Stesura del Report in data: 08/02/2015
Introduzione
Recenti misure sperimentali del Martin Fleischmann Memorial Project (MFMP) hanno messo in evidenza un significativo errore nella misura calorimetrica effettuata sull’Hot-Cat, misura calorimetrica riportata nel documento noto come “TPR2” (Lugano Report). In particolare nel resoconto sperimentale del MFMP viene riportata la seguente considerazione:
“The main revelation was that the emissivity required for the camera to correctly interpret the temperatures on the surface was very close to .95. When we plugged in the emissivities cited from literature in the Lugano report (0.8 to 0.4), the apparent temperature was 1200 to 1500C at 900W in.“
GSVIT già molto tempo addietro aveva avanzato l’ipotesi che le misure e l’analisi calorimetrica effettuata dagli autori (AA) del Report (prof. G.Levi, E.Foschi, B.Höistad, R.Pettersson, Lars Tegnér, H.Essén) contenessero l’errore fondamentale di considerare l’Allumina, dal punto di vista termico EM, come un corpo assimilabile ad un corpo grigio.
Le misure sperimentali, effettuate dal MFMP, eseguite su una loro replica del dispositivo (un simulacro del Hot-Cat), confermano quella ipotesi del GSVIT e se le misure del MFMP sono corrette, si può affermare che il metodo adottato dagli AA del TPR2 per calcolare la temperatura superficiale del reattore (e quindi la quantità di calore irraggiato) era errato.
Quanto l’utilizzo del metodo errato possa pesare sulla misura della temperatura esterna e sulla misura della Potenza irraggiata non è possibile definirlo con precisione, dato che non è sufficiente che il simulacro sia identico nella forma, nelle misure e realizzato anch’esso di Allumina pura. L’Allumina infatti può presentarsi in 7 forme polimorfe con diversa struttura cristallina e industrialmente la dicitura “Allumina pura” è utilizzata già per purezze del 99%. Ricordiamo a questo proposito gli esiti dell’analisi dei campioni di Allumina del Hot-cat eseguiti e riportati nel TPR2:
“The results confirmed that it was indeed alumina, with a purity of at least 99%. Details of this analysis will be found in Appendix 2.“
La presenza di piccole percentuali di impurezze può alterare le caratteristiche (e questo è sfruttato per renderla più adatta alle varie applicazioni) ma non abbiamo trovato in letteratura una influenza determinante di tali impurezze sul valore della Emissività ε.
Nell’ipotesi che l’Allumina utilizzata dal MFMP e quella utilizzata nell’Hot-Cat siano molto simili, l’errore introdotto nella stima della Potenza emessa potrebbe essere dell’ordine di un fattore 2, mentre la temperatura superficiale sarebbe stata sopravvalutata di centinaia di gradi e considerando anche che una misura della temperatura errata ha impatto diretto anche sulla parte di calore ceduto per convezione: Q=h*A*(Ts-Tamb), l’errore sulla stima della Potenza emessa potrebbe essere anche superiore.
Errori di questa entità sarebbero talmente rilevanti da mettere fortemente in discussione il contenuto del Report e le sue conclusioni.
Analisi
Come già messo in evidenza nell’analisi tecnica di Alan Fletcher gli AA adottano per la misura calorimetrica una misura della Potenza irraggiata basata sulla nota legge di Stefan-Boltzmann che lega la Potenza emessa alla (T)4, dove T è la temperatura assoluta di un oggetto. Questa tecnica di misura si basa sulla conoscenza del valore esatto di Emissività della superficie della quale si vorrebbe stimare la temperatura, questo perchè il valore di temperatura del corpo è un elemento fondamentale per il calcolo della Potenza irraggiata secondo la legge di Stefan-Boltzmann.
Gli AA del TPR2 hanno deciso di misurare la temperatura del Hot-Cat utilizzando solo la termocamera (termocamera tipo Optris PI160) e va ricordato che hanno anche affermato che non era possibile posizionare una termocoppia di confronto applicata direttamente sulla superficie del reattore per stabilire dei riferimenti affidabili dell’effettiva temperatura:
“We also found that the ridges made thermal contact with any thermocouple probe placed on the outer surface of the reactor extremely critical, making any direct temperature measurement with the required precision impossible.“
(una affermazione questa già contestata all’epoca perchè incomprensibile, il fatto che il MFMP invece sia riuscito nell’intento smentisce di fatto quelle loro affermazioni) ed hanno deciso di calibrare la termocamera, utilizzata per la misura della temperatura superficiale, basandosi sul seguente procedimento:
-
si rileva il valore della temperatura indicato dalla termocamera e con quello si entra nel diagramma che associa l’Emissività alla temperatura dell’Allumina pura (Figura 6 del TPR2)
-
successivamente sul diagramma si controlla se quel valore di Emissività corrisponde effettivamente al valore di temperatura letta.
-
supponendo che non corrisponda, si varia l’impostazione dell’Emissività sulla termocamera fino a trovare il valore che porta alla coincidenza tra il valore di temperatura indicato dalla termocamera e il valore di temperatura in ordinata sul diagramma Emissività/Temperatura relativo all’Allumina
-
ed infine si imposta nella termocamera un valore di Emissività pari a quell’ipotetico valore
Questo metodo sarebbe corretto se la superficie dell’Allumina si comportasse come un corpo grigio e nell’ipotesi che i dati del diagramma utilizzato [relativi all’Emissività Totale (Nota1)] si riferissero ad una Allumina identica a quella effettivamente utilizzata. Si ricorda che l’Emissività ε di un materiale è la frazione di energia irraggiata dal materiale rispetto all’energia irraggiata da un corpo nero alla stessa temperatura. Assunta unitaria l’Emissività del corpo nero un qualunque oggetto reale ha Emissività inferiore: se il valore non dipende dalla lunghezza d’onda λ tale materiale viene denominato corpo grigio. Se il valore dell’Emissività invece varia apprezzabilmente in funzione della lunghezza d’onda non si può definire tale materiale come corpo grigio. Questo è, ad esempio, il caso dell’Allumina.
Gli AA sostanzialmente non hanno adottato nessuna delle tecniche suggerite da Optris GmbH (IR camera manufacturer) a pagina 10 di questo documento, al fine di stimare il corretto valore dell’Emissività:
Experimental Determination of Emissivities In the addendum you will find emissivity dates for various materials from technical literature and measurement results. There are different ways to determine the emissivity.
Method 1: With the help of a thermocouple. With the help of a contact probe (thermocouple) an additional simultaneous measurement shows the real temperature of an object surface. Now the emissivity on the infrared thermometer will be adapted so that the temperature displayed corresponds to the value shown with the contact measurement. The contact probe should have good temperature contact and only a low heat dissipation.
Method 2: Creating a black body with a test object from the measuring material. A drilled hole (drilling depth ≤ ⅓) in thermal conducting material reacts similar to a black body with an emissivity near 1. It is necessary to aim at the ground of the drilled hole because of the optical features of the infrared device and the measuring distance. Then the emissivity can be determined.
Method 3: With a reference emissivity. A plaster or band or paint with a known emissivity, which is put onto the object surface, helps to take a reference measurement. With an emissivity thus adjusted on the infrared thermometer the temperature of the plaster, band or paint can be taken. Afterwards the temperature next to this surface spot will be taken, while simultaneously the emissivity will have to be adjusted until the same temperature is displayed as is measured beforehand on the plaster, band or paint. Now the emissivity is displayed on the device.
Gli AA si sono avvalsi degli specifici “Dots” (il cui valore di Emissività è noto) solo per quanto riguarda la misura di alcune parti (i cable rods) i cui materiali (a temperature molto inferiori) non sono stati analizzati e verificati:
“Dots” of known emissivity, necessary to subsequent data acquisition, were placed in various places on the cable rods. It was not possible to perform this operation on the dummy reactor itself (and a fortiori on the E-Cat), because the temperatures attained by the reactor were much greater than those sustainable by the dots.
…
It was not possible to extract any sample of the material constituting the rods, as this is firmer than that of the reactor.
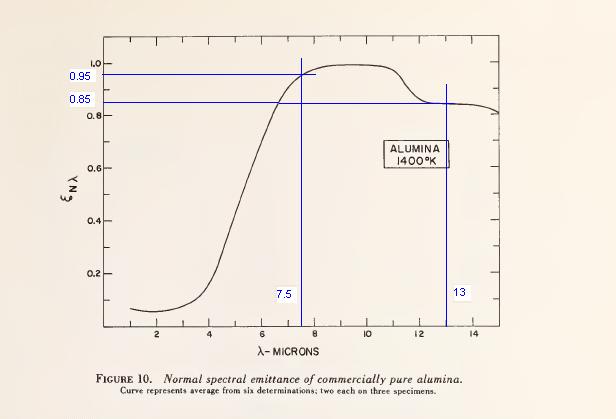
Va rilevato che in letteratura (vedere Figura 1) sono noti i valori di Emissività spettrale dell’Allumina (Al2O3) ed in particolare quelli nella banda di misura della termocamera Optris OP160, banda che va da 7.5 a 13 µm.
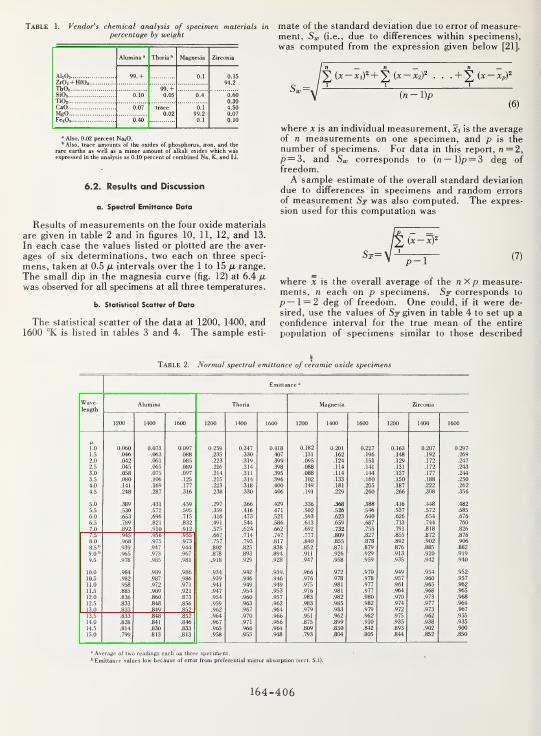
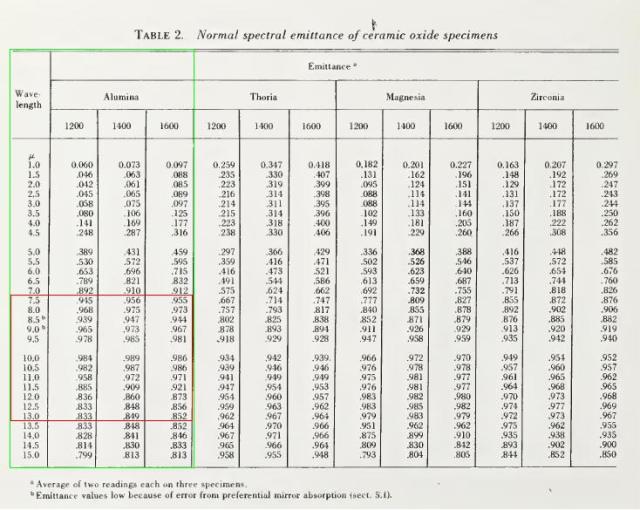
I valori di Emissività ε = f(λ,T) sono documentati nel pubblicazione del 1971 del U.S. Department of Commerce National Bureau of Standard, volume 7:
Precision Measurement and Calibration – Radiometry and Photometry
Figura 1 – NBS Precision Measurement and Calibration Photometry and Radiometry
e come mostrato in Figura 2A,2B e Figura 3 ad esempio per temperature comprese tra 1200 e 1600 K cioè da circa 930 a 1330 °C, l’Emissività Spettrale assume un valore misurato compreso tra 0.85 e 0.95 nel campo di misura della termocamera.
Figura 2A – Alumina (99+) Emittance vs Wavelenght and Temperature
Figura 2B – Table 2 details
Figura 3 – Alumina (99+) Emittance vs Wavelenght @ 1400 K
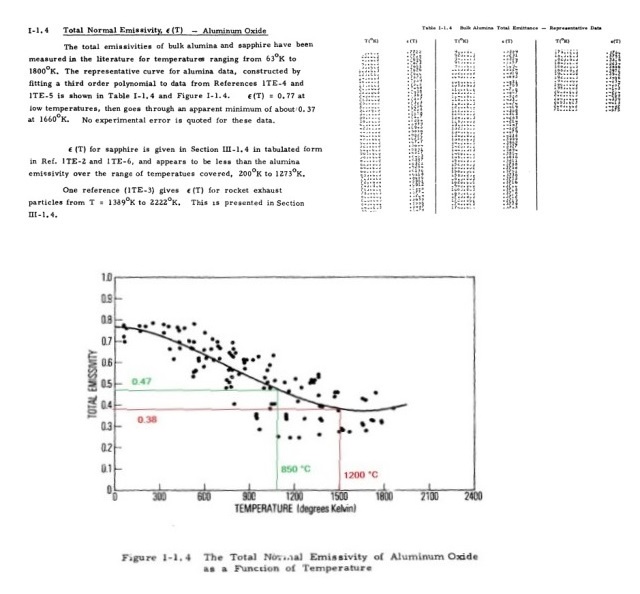
Oltre alla letteratura scientifica, anche i risultati delle misure effettuate dal MFMP mostrano come il valore di Emissività Spettrale dell’Allumina del loro simulacro vari grandemente in funzione della lunghezza d’onda λ, per lunghezze d’onda prossime ai 10 µm, cioè nel campo letto dalle normali termocamere, tale valore risulta circa 0.95, valori sostanzialmente confermati anche dal documento: Handbook of the Infrared Optical Properties of Al2O3. Carbon, MGO and ZrO2. Volume 1 (di cui uno stralcio è reperibile a questo link), mentre il valore misurato di Emissività Totale (vedere Figura 4) da utilizzare per il calcolo della potenza irraggiata, per una T intorno ai 1000°C, risulta meno della metà. Si noti come proprio nell’intorno di queste temperature (che sono quelle probabilmente assunte dall’Hot-Cat durante il test) si abbia il minimo di emissività, che in qualche misurazione risulta essere inferiore a 0.3.
Figura 4 – Al2O3 Total Emissivity vs Temperature
Inoltre queste misure mostrano come la dispersione reale dei dati di Emissività Totale, a parità di temperatura, vada ben oltre l’errore e l’incertezza che gli AA citano nel TPR2:
The error associated with the plot’s trend has been measured at ± 0.01 for each value of emissivity: this uncertainty has been taken into account when calculating radiant energy.
ed anche R.Morrell, autore del testo preso a riferimento [3] dagli AA, nel suo libro: Handbook of properties of technical & engineering ceramics, Part 2, precisa a pagina 88, a commento del suo grafico di pagina 87 Figura A4.10 (quello posto come Figura 6 del TPR2 e che poi ha dato origine al Plot1 del TPR2), mettendo in guardia il lettore dal prendere quel grafico troppo alla lettera:
“Such data should be considered tentative because it is known that emissivity can vary with grain size, porosity and surface finish through varying degrees of optical translucency and scattering.“
La questione principale rimane comunque quella che gli AA avrebbero dovuto utilizzare il valore di Emissività Spettrale per le misure con la termocamera (ad esempio 0.90–0.95 similmente ai valori rilevati dal MFMP) mentre il valore dell’Emissivita’ Totale per il calcolo della Potenza irraggiata applicando la formula di Stefan-Boltzmann (tipicamente 0.40 ad alta temperatura). Si noti come queste questioni dimostrano quanto delicata (e per certi versi poco oculata) sia stata la scelta di adottare questo tipo di calorimetria.
Il valore di Emissività da utilizzare per la termocamera risulta molto superiore a quello da utilizzare per il calcolo della Potenza irraggiata. Se si considera una temperatura di esercizio di 1000°C, il picco spettrale di emissione massima (picco di Wien), si trova a circa 2.3 µm.
Blackbody Wien displacement Spectrum @ T=1000°C
Dal momento che l’Emissività Totale dell’Allumina, come anche riportato nella Figura 6 del Report, diminuisce all’aumentare della temperatura (cioè al diminuire della lunghezza d’onda del picco di emissione), l’Emissività Totale da utilizzare per il calcolo della potenza coincide effettivamente col valore indicato dal diagramma (a 1000°C indica circa 0.4), mentre nel caso della misura tramite termocamera, anche se stiamo osservando un corpo a 1000°C, il valore di Emissività da utilizzare (cioè l’Emissività nello Spettro di misura della termocamera) sarà comunque quello che compete al campo di lettura della termocamera utilizzata (7.5-13 µm in questo caso).
Come già sottolineato in altre occasioni, al fine di ridurre il problema dell’errore di Emissività, in fonderia e nell’analisi dei forni non si utilizzano delle normali termocamere (come invece hanno utilizzato gli AA), ma le termocamere con finestra di lettura nel campo 3-5 µm. In questo caso la scelta di una termocamera con finestra di lettura 7.5-13 µm per taluni aspetti appare condizionata dal fatto che solo in quel campo spettrale l’Allumina presenza Emissività prossima a 1.
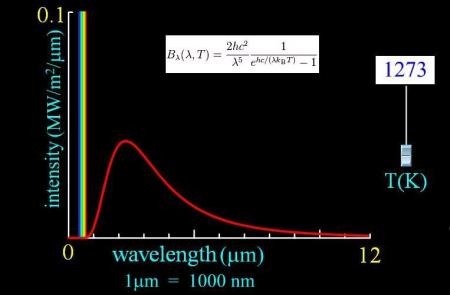
A titolo di esempio in Figura 5 è riportata l’Irradianza Spettrale alla temperatura di 1200K.
Per un confronto immediato sono stati calcolati e riportati:
a) in blu lo Spettro di un Corpo Nero @ T=1200K
b) in grigio lo Spettro che un Corpo Grigio @ T=1200K, di Emissività Totale 0.45
c) in rosso lo Spettro del corpo di Allumina secondo i dati di Emissività Spettrale del Al2O3 @ T=1200K, ricavato sulla base dei dati del National Bureau of Standard (vedere Figura 2). I valori ε = f(λ) mancanti sono stati ottenuti per interpolazione.
Figura 5 – Planck’s Spectrum 1200K
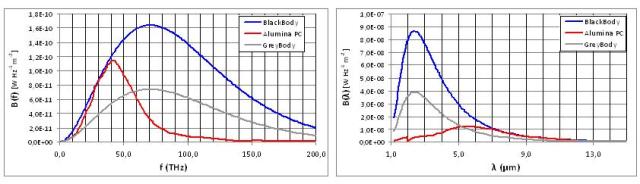
Integrando lo Spettro per il Corpo Nero @ T=1200K si ottiene il valore teorico di Irradianza (Radiant Power RP) pari a 117573 W/m2. Integrando invece solo l’area dello Spettro che cade all’interno del range spettrale di misura della Termocamera (che ricordiamo essere 7.5–13 µm), si ottiene il valore di RP nella banda di misura. In queste condizioni per effetto dei valori utilizzati, risulta evidente che il Corpo Grigio con Emissività 0.45 (valore settato in accordo con quanto riportato nel Plot1 del TPR2 @ T 1200K) presenta irradiazione largamente inferiore rispetto al Corpo di Allumina pur essendo alla medesima Temperatura di 1200K.
In queste condizioni per Corpo Nero la RP vale 9.96kW/m2 e calcolando il rapporto tra la RP dell’Allumina 9.4kW/m2 e quella del Corpo Grigio 4.48kW/m2, si ottiene un fattore 2.1 che testimonia la presenza dell’errore di misura dovuto all’errato utilizzo dei parametri di Emissività.
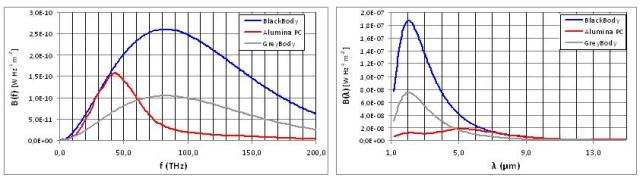
Analogamente in Figura 6 è riportata l’Irradianza Spettrale alla temperatura di 1400K. Come in precedenza per un confronto immediato sono stati calcolati e riportati:
a) in blu lo Spettro di un Corpo Nero @ T=1400K
b) in grigio lo Spettro che un Corpo Grigio @ T=1400K, di Emissività Totale 0.4
c) in rosso lo Spettro del corpo di Allumina secondo i dati di Emissività Spettrale del Al2O3 @ T=1400K, ricavato sulla base dei dati del National Bureau of Standard (vedere Figura 2). I valori ε = f(λ) mancanti sono stati ottenuti per interpolazione.
Figura 6 – Planck’s Spectrum 1400K
Analogamente integrando lo Spettro per il Corpo Nero @ T=1400K si ottiene il valore teorico di Irradianza (Radiant Power RP) pari a 217819 W/m2. Integrando invece solo l’area dello Spettro che cade all’interno del range spettrale di misura della Termocamera (che ricordiamo essere 7.5–13 µm), si ottiene il valore di RP nella banda di misura. In queste condizioni per effetto dei valori utilizzati, risulta evidente che il Corpo Grigio con Emissività 0.4 (valore settato in accordo con quanto riportato nel Plot1 del TPR2 @ T 1400K) presenta irradiazione largamente inferiore rispetto al Corpo di Allumina pur essendo alla medesima Temperatura di 1400K.
In queste condizioni per Corpo Nero la RP vale 13kW/m2 e calcolando il rapporto tra la RP dell’Allumina 12.4kW/m2 e quella del Corpo Grigio 5.2kW/m2, si ottiene un fattore 2.38 che testimonia la presenza dell’errore di misura dovuto all’errato utilizzo dei parametri di Emissività.
Notare che i diagrammi a sinistra nelle due Figure 5 e 6 mostrano l’andamento dello spettro di Planck in funzione della frequenza (f). Data la caratteristica di proporzionalità inversa tra frequenza e lunghezza d’onda, la parte sinistra del diagramma in funzione della lunghezza d’onda (λ) [il diagramma posto sulla destra] corrisponde alla parte destra del diagramma in funzione della frequenza e viceversa.
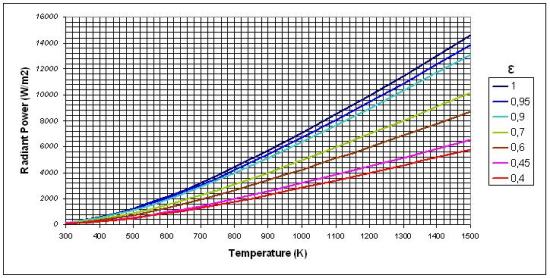
La Figura 7 mostra il legame tra Radiant Power e la Temperatura riferita ad una misurazione nel range spettrale 7.5–13 µm. La curva color nero rappresenta appunto la Radiant Power del Corpo Nero che fa da riferimento e curva di calibrazione per la termocamera.
Il grafico ha a parametro l’Emissività ε al fine di mostrare quanto essa incida sulla stima della reale temperatura del corpo quando quest’ultima venga misurata utilizzando questo tipo di metodologia con termocamera IR.
Figura 7 – Radiant Power Vs Temperature and Emissivity (Spectral range 7.5-13 µm)
Si consideri ad esempio la temperatura T1 di 1100K rilevata con una termocamera nella quale sia stata settata (erroneamente) una Emissività di 0.45 al posto del valore corretto 0.90.
La RP desumibile dal grafico di Figura 7 per una ε=0.45 (circa 4kW/m2) è in realtà quella che compete alla curva ε=0.90 ma con una Temperatura effettiva T2 di soli 800K (sovrastima della temperatura di 300K).
Sulla base di questi valori di temperatura, se si applica la relazione Stefan-Boltzmann: P=ε*σ*(T^4-Tamb^4) allo scopo di calcolare la potenza termica radiata da un corpo per unità di superficie (σ=5.67*10^-8 [W/(m2*K4)] e Tamb 300K, cioè 27°C), si ottiene:
Pmeas(T1) = ε1*σ*(1100^4-300^4) = 40.4 [kW/m2]
Preal(T2) = ε2*σ*(800^4-300^4) = 14.7 [kW/m2]
per eseguire il raffronto della Potenza irradiata con la SB va considerata l’Emissività Totale (per queste temperature da Plot1 del TPR2 ε1=0.49 e ε2=0.65). Il rapporto tra Pmeas e Preal vale 2.7 e questo risultato indica una grande sovrastima della Potenza termica irradiata dal corpo del quale invece si vorrebbe valutare con precisione il calore ceduto all’ambiente per irradiazione elettromagnetica.
Ma l’errore può essere anche superiore. Si consideri ad esempio una temperatura T1 di 1320K (circa 1050°C) come rilevata dalla termocamera nella quale sia stato settato (erroneamente) il valore di Emissività di 0.42 desunto dal Plot1 del TPR2 al posto del valore corretto 0.90.
La RP desumibile dal grafico di Figura 7 per una ε compresa tra 0.40 e 0.45 (circa 4.8kW/m2) è in realtà quella che compete alla curva ε=0.90 ma con una Temperatura effettiva T2 di soli 880K (sovrastima della temperatura di 440K).
Sulla base di questi valori di temperatura, applicando poi la relazione Stefan-Boltzmann si ottiene:
Pmeas(T1) = ε1*σ*(1320^4-300^4) = 72.1 [kW/m2]
Preal(T2) = ε2*σ*(880^4-300^4) = 19.8[kW/m2]
come nell’esempio precedente per la SB si considera l’Emissività Totale (per queste temperature da Plot1 del TPR2 ε1=0.42 e ε2=0.59). Il rapporto tra Pmeas e Preal risulta 3.6 cioè ancora una enorme sovrastima della Potenza termica irradiata dal corpo e se, in queste condizioni, si considerassero valori di Tmeas della termocamera ancora superiori, non si puo’ escludere che i risultati in termine di errore (che continua ad incrementarsi velocemente, come pure la sovrastima della Potenza termica) sarebbero ancora peggiori.
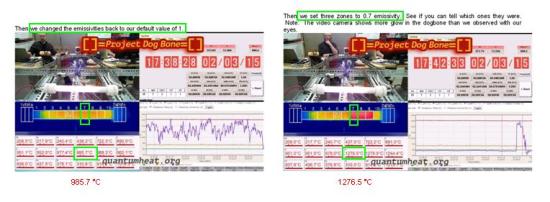
Ritornando per un attimo alle misure e ai dati del resoconto del MFMP è interesante verificare come quella esposta non sia solo teoria. Il Test case del MFMP è rappresentato in Figura 8.
Figura 8 – MFMP Test case
Il MFMP ha operato una variazione del valore di Emissività, modificando il settaggio sulla termocamera, applicandolo per confronto solo ad alcune zone osservate. Il valore è stato variato da 1 a 0.7 per le zone n.7, n.8 e n.9.
Consideriamo ad esempio la zona n.7 del dispositivo inquadrato dalla telecamera. L’effetto conseguente sulla temperatura indicata dalla temocamera è che i valori letti passano da 985.7°C a 1276.5°C (un variazione di oltre 290°C).
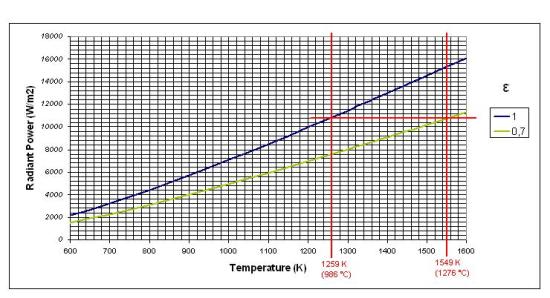
La figura seguente (Figura 9, ampliata rispetto alla precente Figura 7 per rappresentare meglio la zona di interesse) mostra l’esistenza di un buon accordo tra i dati sperimetali del MFMP e il calcolo dell’errore di temperatura che ci si aspetterebbe a fronte di quel erroneo settaggio dell’Emissività, dovuto ad esempio all’incertezza sul valore effettivo che è da applicare.
Figura 9 – Temperature error vs Emissivity in MFMP test condition (Spectral range 7.5-13 µm)
Infine applicando a questo Test case la SB ed utilizzando i dati di Emissività Totale (come da Plot1 del TPR2), si ricaverebbe una sovrastima della Potenza termica effettivamente irradiata di un fattore 2.6.
Verifica sperimentale tubo di Allumina
Una ulteriore verifica sperimentale del fatto che l’Emissività dell’Allumina nel campo 8-14 µm vale circa 0.95 è stata ottenuta eseguendo un semplice test che fa uso di un Pirometro (non avendo a disposizione una termocamera).
Come si può verificare consultando l’Instruction Sheet dello strumento, il Pirometro 80T-IR della Fluke ha una finestra spettrale di risposta 8-14 µm molto simile a quella della termocamera utilizzata dagli AA nel TPR2 (7.5-13 µm) e lo strumento è calibrato per una Emissività pari a 0.95.
Poiché il limite operativo di temperatura per tale strumento è di 260°C si è deciso di limitare la temperatura dell’allumina a circa 160°C. L’uscita analogica del Pirometro, pari a 1mV/°C , è stata collegata a un milliVoltmetro con fondo scala 200mV.
Secondo la bibliografia la curva dell’Emissività spettrale dell’Allumina è poco influenzata dalla temperatura per cui la misura risulta comunque significativa. Gli stessi AA hanno eseguito quella che secondo loro era la calibrazione alla temperatura di 450°C mentre le misure del Hot-Cat sono state eseguite a temperature decisamente superiori.
Si è utilizzato un tubo in Allumina pura (99.7%) della Sceram, diametro esterno 27mm, diametro interno 20mm, lunghezza 150mm (codice AAH01700, tipo C799 – DIN VDE 0335).
All’interno del tubo, come visibile nelle Figure I e II sono state inserite 4 resistenze da 68 ohm 10W in ceramica, collegate in parallelo.
Figura I
Figura II
Le resistenze sono state alimentate in Corrente Continua mediante alimentatore stabilizzato. Per garantire un buon scambio di calore tra le resistenze e il tubo in Allumina si è riempita ogni cavità interna mediante polvere secca di cemento Potland, come visibile in Figura III.
Figura III
All’interno del tubo di Allumina è stata posta una termocoppia tipo K collegata a un termometro, come visibile in Figura IV.
Figura IV
Come visibile in Figura V, l’intero sistema è stato coibentato mediante lana di roccia per ridurre lo scambio termico garantendo così una notevole uniformità di temperatura.
Figura V
Nella zona centrale l’isolamento termico viene interrotto per permettere la lettura della temperatura superficiale del tubo mediante il Pirometro ottico.
La tensione dell’alimentatore è stata regolata per far sì che il sistema si stabilizzasse alla temperatura di circa 160°C (potenza circa pari a 10W), poi sono state eseguite le letture comparative. Per maggior sicurezza, una volta raggiunta la stabilità termica, sono state eseguite 3 letture a distanza di decine di minuti (Figure VI, VII, VIII), le tre misure hanno fornito risultati molto simili.
Figura VI
Figura VII
Figura VIII
La coibentazione non è stata particolarmente curata dal momento che la presenza di una dissipazione termica, quindi di un gradiente termico tra la zona interna misurata dalla termocoppia e la superficie misurata dal termometro, porta al limite ad una stima del valore di Emissività inferiore al reale.
La temperatura letta dal Pirometro è risultata inferiore a quella letta dalla termocoppia di circa 5°C, differenza in parte imputabile al flusso termico. Trascurando la differenza di temperatura derivante da tale flusso e considerando che lo strumento è calibrato per una Emissività di 0.95, l’effettiva Emissività del tubo di Allumina risulta in prima approssimazione pari a:
ε= 0.95* [(160 + 273) ]^4 / [(165 + 273) ]^4 = 0.907
A questa temperatura, utilizzando i valori di Emissività del TPR2 che a 160°C risultava valere circa 0.70, l’errore di lettura del Pirometro sarebbe stato di circa 34°C.
Conclusioni
I dati sperimentali ricavati dal MFMP sono in accordo con quelli presenti in letteratura e confermano che la procedura ed i valori di Emissività, utilizzati dagli AA del TPR2 per le misure con la termocamera, sono errati. Il test sperimentale GSVIT ha ulteriormente dimostrato che l’Emissività Spettrale dell’Allumina pura, nel campo di lettura della termocamera utilizzata durante i test sull’Hot-Cat, è superiore a 0.90. Questi dati risultano molto diversi da quelli diagrammati ed utilizzati nel TPR2 dagli AA che risultano essere quelli relativi all’Emissività Totale dell’Allumina. Nel range di temperature 1200-1400°C il Plot1 del TPR2 fa riferimento ad una Emissività di circa 0.40 mentre secondo la letteratura l’Emissività Spettrale, nel campo di lettura della termocamera, si mantiene intorno a valori prossimi a 0.95. Questo genere di errore può portare ad una notevole sovrastima della temperatura superficiale e ad una sovrastima della Potenza termica di un fattore 2 o più. Un errore di queste proporzioni (che alla luce delle misure eseguite appare probabile) rende i risultati delle misure del calore prodotto dal Hot-Cat, riportate nel TPR2, a nostro avviso non attendibili, mentre sarebbe stata fattibile una semplice ed accurata Calorimetria a flusso similmente a quella illustrata nel precedente Post.
Gruppo Scientifico per la Valutazione Indipendente di Tecnologie 