ENEA Rapporto 41 – Analisi e critica tecnica del contenuto | Gruppo Scientifico per la Valutazione Indipendente di Tecnologie

Stesura del Report in data: 14/12/2016

Pubblicazione con pw: 03/01/2017

Aggiornamenti: 25/01/2017 e 16/03/2017

Pubblicazione senza pw: 25/03/2017

INDICE

Premessa

1 – La cella utilizzata

2 – I punti deboli del documento

A – La forma del catodo
B – La misura del caricamento
C – La misura dell’Elio 4
D – La misura del calore in eccesso
E – Misura di raggi gamma

3 – La fusione del catodo

4 – Note tecniche esplicative (dalla Nota 1 alla Nota 28)

5 – Conclusioni

Appendice A – Verifica sperimentale della possibilità di arroventare un sottile filo metallico immerso in acqua.

Appendice B – Verifica sperimentale della possibilità di realizzare un efficiente calorimetro isoperibolico.

Appendice C – Verifica sperimentale dell’influenza della tensione utilizzata per la misura della resistenza del catodo.

Premessa

Nell’anno 2002 l’ENEA di Frascati pubblicò un Report dal titolo “Experimental evidence of 4He production in a cold fusion experiment” (noto anche come Rapporto 41) relativo ad una sperimentazione tenutasi nei tre anni precedenti. La sperimentazione era stata commissionata da Carlo Rubbia con lo scopo di sondare la possibilità di ottenere reazioni di fusione nucleare a temperatura ambiente (la cosidetta Fusione Fredda).Il gruppo di ricerca, condotto dalla dott.sa Antonella de Ninno, giunse alla conclusione che la fusione Deuterio-Deuterio all’interno di un reticolo di Palladio e l’effetto Preparata (che fa riferimento all’effetto Coehn-Aharanov) erano ampiamente dimostrati. Ciononostante la comunità scientifica non prese in considerazione la loro relazione e nessuna rivista scientifica la pubblicò portando gli autori a dichiarare che nella migliore delle ipotesi la ricerca era stata affossata deliberatamente (Nota 1). In una intervista di alcuni anni fa Antonella de Ninno affermava:

“Nessuno che abbia detto: , , quindi se la nostra misura è sbagliata, noi non sappiamo perché” (Nota 2).

Dopo 15 anni dalla pubblicazione abbiamo pensato di analizzare il documento nel tentativo di dare una risposta al dubbio degli stessi sperimentatori (Nota 3).

1 – La cella utilizzata

I test cui si riferisce il Rapporto 41 sono stati realizzati mediante una piccola cella elettrolitica (8.5 cc) con anodo piano in Platino e catodo quasi monodimensionale in Palladio immersi in soluzione di deuterossido di Litio (LiOD). Si tratta quindi di una cella Palladio – Deuterio concettualmente simile a quella utilizzata dai precursori Fleischmann e Pons tredici anni prima, ma con una particolare costruzione del catodo in grado, a detta degli autori, di aumentare grandemente la quantità di Deuterio introdotta nel reticolo del Palladio, a seguito del cosiddetto “effetto Preparata”, rendendo il fenomeno della fusione nucleare quasi immediato e molto ripetibile.

2 – I punti deboli del documento

La ricerca aveva un obiettivo ben preciso: correlare la quantità di ⁴He (Nota 4) prodotta da una cella elettrolitica (dotata di catodo di Palladio e elettrolita di acqua pesante resa elettricamente conduttiva mediante un composto del Litio) con il calore prodotto in eccesso. Si noti che secondo la fisica nota nessuno dei due fenomeni avrebbe dovuto verificarsi, quindi cercare in più una correlazione quantitativa era un obiettivo oltremodo ambizioso, che avrebbe confermato al di là di ogni ragionevole dubbio l’esistenza del fenomeno (Nota 5).I punti a nostro avviso criticabili che emergono dalla lettura del documento sono i seguenti:

A – La forma del catodo

Dal momento che si sarebbero dovuti misurare sia il calore che l’Elio prodotti, non si capisce perchè non si sia cercato di massimizzare la quantità di Palladio presente sul catodo e si sia deciso di utilizzare un catodo che ne conteneva una quantità così piccola (circa 1 mg).

Anche mantenendo la stessa dimensione dell’intera cella e la stessa forma unidimensionale del catodo, non si capisce perchè non si sia adottato un “passo” più stretto della serpentina che lo costituiva. Come si vede nelle Figure 2b e 10 del rapporto, la larghezza della pista di palladio depositata sul substrato era di circa 50 μm, spaziata di circa 800 μm: si sarebbe potuto adottare un passo di 150 – 200 μm aumentando così la quantità di Palladio di circa cinque volte. Inoltre non è chiaro perchè si sia adottata una singola serpentina molto lunga (1 metro), incorrendo nel rischio di fondere la parte attraversata dall’intera corrente (cosa effettivamente verificatasi come si mostrerà più avanti). Anche ammesso esista un valido motivo per mantenere proprio quella lunghezza, sullo stesso supporto avrebbero potuto trovare spazio senza alcun problema cinque serpentine in parallelo. Con una massa cinque volte superiore di Palladio si sarebbe aumentata di 5 volte sia la quantità di Elio eventualmente prodotta, sia la quantità di calore in eccesso riducendo le incertezze delle misure mentre il costo e la complessità del sistema sarebbero rimasti pressocché invariati.

B – La misura del caricamento

Secondo gli autori, il fenomeno di fusione nucleare del Deuterio inizierebbe solo quando il rapporto tra gli atomi di Deuterio all’interno del reticolo del Palladio e il numero di atomi di Palladio ha superato il valore critico di 1 (Nota 6).

La misura del livello di caricamento del Palladio (rapporto [D]/[Pd]) è stata effettuata mediante misura della resistività del catodo. Sebbene la procedura descritta e i dati riportati portino a pensare che gli autori possano veramente essere riusciti a caricare il Palladio a valori mai visti prima in letteratura (addirittura superiori a x = 1), tre particolari portano ad avere dubbi a riguardo.

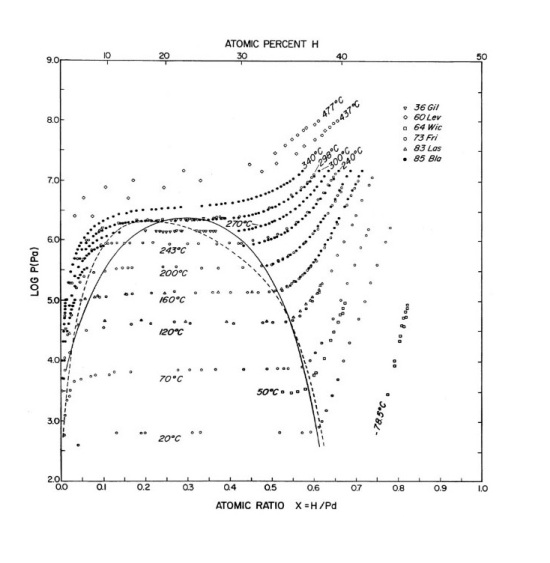
Il primo è che il catodo non era sottoposto durante l’elettrolisi, a campo elettrico simmetrico. Il catodo infatti era depositato su un substrato isolante sotto forma di sottile pista bagnata dall’elettrolita solo sulla faccia esterna (larga circa 50 μm) e sulle due facce laterali (alte circa 2 μm). Il Deuterio aveva modo quindi di entrare solo attraverso tali superfici. La superficie in stretto contatto col substrato invece non era soggetta nè al contatto con l’elettrolita né all’azione del campo elettrico. In accordo con la letteratura nota (e per diretta esperienza di GSVIT nel test di compressione elettrochimica consultabile qui) in queste condizioni il Deuterio entrato nel Palladio tende ad uscire dalla superficie non esposta all’elettrolisi esercitando una pressione che è ricavabile dal diagramma di stato Palladio – Deuterio e che con valore di x pari a 0.85 a temperatura ambiente è superiore a 500 bar, per superare (presumibilmente perché mai ottenuto in laboratorio) i 10.000 bar per x pari a 0.95. Ci si deve quindi chiedere come abbia fatto il sottile film di Palladio a non distaccarsi dal substrato.

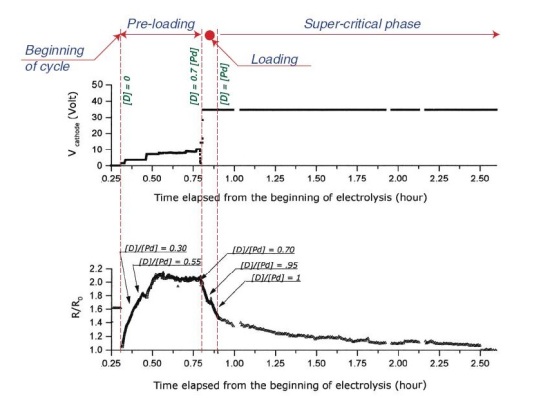
Il secondo motivo di dubitare della realtà di tali livelli di caricamento deriva dall’analisi della Figura 8 del rapporto, che riportiamo di seguito.

Figura 8 del Rapporto 41

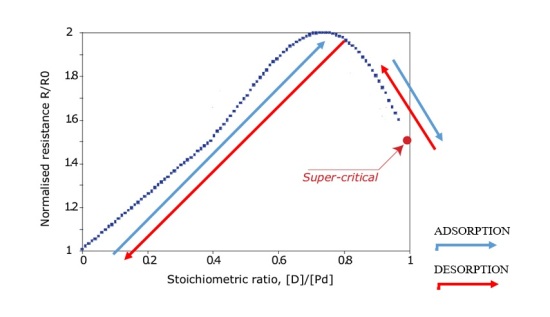
In essa si notano interruzioni, della durata di circa 2 minuti, della curva che esprime il rapporto R/R0 dalla quale gli autori desumono il livello di caricamento utilizzando il noto diagramma (comunemente detto di Baranowsky) riportato in Figura 7 del documento (Nota 7) che si suppone corrispondano alle interruzioni della elettrolisi citate nel testo e effettuate durante la fase supercritica allo scopo di verificare se effettivamente il sistema si trovasse a destra o a sinistra del massimo del rapporto R/R0. Dato lo spessore piccolissimo della pista di Palladio, si deve supporre che, soprattutto a livelli di caricamento così alti, il tempo di rilascio del Deuterio durante la pausa nell’elettrolisi dovesse essere molto breve. Non è chiaro quindi come mai la curva R/R0 ogni volta riprenda praticamente dallo stesso valore raggiunto al momento dell’arresto dell’elettrolisi o addirittura da un valore più basso come si nota nell’ultima interruzione (Nota 8).

Il problema della misura del caricamento di un catodo di Palladio era stato ampiamente trattato in una tesi di laurea in fisica all’università di Milano nell’anno accademico 1999/2000, relatore Luigi Zanotti, nella quale la stessa De Ninno appare come correlatore esterno (Analisi Sperimentale e Teorica del Caricamento in Idrogeno e Deuterio di Film di Palladio, Codici PACS 11.00,66.30, 72.80.G,81.40.R). Tale tesi, che sembra essere stata la base di riferimento per l’intero esperimento realizzato a Roma pochi anni dopo (eccetto per la mancanza della ricerca dell’Elio), appare di tutt’altro spessore e molto ben documentata (Nota 9).

In tale tesi, la misura del caricamento del catodo era effettuato in identico modo. Vi si legge che tempi troppo brevi portavano a errori inaccettabili della misura anche a causa delle correnti di elettrolisi che non avevano il tempo di azzerarsi, mentre tempi troppo lunghi portavano a degassamento del catodo: per questo la misura della conducibilità elettrica del catodo era effettuata con interruzioni dell’elettrolisi per tempi che oscillavano da 50ms (pag. 20 della tesi) a 800ms (pag. 66 della tesi). Nella stessa tesi si legge come la misura della conducibilità del catodo effettuata con catodo immerso in una soluzione elettricamente conduttrice (che quindi costituisce una resistenza elettrica incerta in parallelo) portasse a una sovrastima della variazione di resistività del catodo (cosa che, come descritto al capitolo 4.5 della tesi, li spinse a effettuare misure con caricamento gassoso a temperatura criogenica, che, ovviamente, eliminava il problema). Nel Rapporto 41 dell’ENEA non vi è traccia del fatto che gli autori abbiano affrontato il problema.

Nella tesi milanese si legge che non furono mai in grado di raggiungere il rapporto x = 1, pur essendo il sistema praticamente identico. Al contrario nel Rapporto 41 in esame si asserisce che tale valore fu ampiamente e ripetutamente superato, tanto che nella Figura 8 del Rapporto si può notare come dopo 2.5 ore di fase supercritica (cioè con x>1), la resistenza del catodo era addirittura tornata esattamente e stabilmente pari a quella del catodo non caricato (R/R0 = 1). Si noti che non è possibile dire a che livello di caricamento questo corrisponda, dato che non esiste alcun diagramma di stato “ufficiale” con valori di x maggiori di 0.9 (Nota 10).

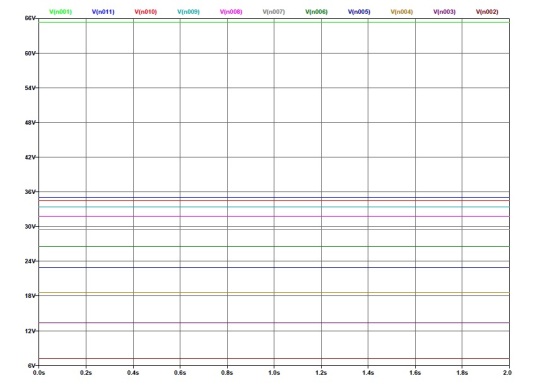
Gli autori, anche considerando il fatto che in pochissimi hanno dichiarato il raggiungimento di valori di caricamento pari o superiori a 1, valore ritenuto dalla maggioranza dei chimici impossibile, avrebbero dovuto riportare i valori R/R0 anche durante i momenti di interruzione dell’elettrolisi e soprattutto continuare a registrare tale rapporto anche alla fine dell’esperimento, una volta spenta definitivamente l’elettrolisi. La curva avrebbe dovuto, nel giro di pochi minuti risalire circa al valore R/R0 = 2, per poi ridiscendere al valore R/R0 = 1 una volta completato il degassamento, come mostrato in Figura 1:

Figura 1

Lascia perplessi il fatto che in tre anni e con (si suppone) molti esperimenti eseguiti, gli autori non abbiano mai pensato di documentare in maniera inequivocabile l’effettivo raggiungimento di questa fase supercritica. Soprattutto se si considera che è ritenuta dagli autori una condizione fondamentale per l’innesco del fenomeno della fusione.

Il terzo particolare che porta a dubbi sul livello di caricamento raggiunto riguarda il valore di resistenza del catodo. Al punto 2 del documento gli autori dichiarano che la resistenza del catodo a temperatura ambiente e senza alcun caricamento di Deuterio era pari a 3 kΩ mentre nella riga precedente dichiarano che il catodo era costituito da uno strato di Palladio largo 50 μm spesso 2 μm e lungo 1 metro. Come è facile verificare, la resistenza di un simile catodo dovrebbe essere di circa 1050 Ω. Una simile differenza avrebbe richiesto una spiegazione da parte degli autori che invece sembrano non essersi nemmeno accorti del problema.

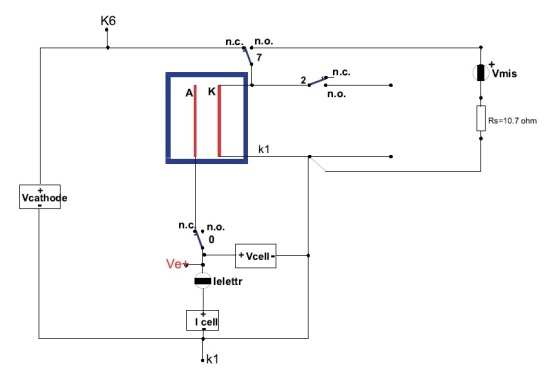
La resistenza del catodo veniva misurata, a elettrolisi interrotta, mediante un generatore ausiliario di tensione continua in serie ad una resistenza da 10.7 Ω, come si può vedere nella Figura 3 del documento che per comodità riportiamo di seguito (Nota 11).

Figura 3 del Rapporto 41

C – La misura dell’Elio 4

La principale difficoltà nel misurare la quantità di ⁴He eventualmente prodotto dalla cella è legata al fatto che l’elettrolisi dell’acqua pesante produce Ossigeno e Deuterio e quest’ultimo ha peso molecolare che differisce da quello dell’Elio 4 solo dello 0.6% (4He = 4.0026 amu; De2 = 4.0282 amu). Per individuare quali elementi erano presenti nel gas in uscita dalla cella è stato utilizzato un analizzatore di massa a quadrupolo ad alta risoluzione (QMA) che evidenzia con delle righe su un diagramma la presenza dei vari elementi (Nota 12). Tale diagramma ha il peso atomico in ascissa e una corrente in ordinata, corrente che è proporzionale (a meno di piccoli fattori correttivi dipendenti dalla diversa sensibilità dello strumento per ogni tipo di gas) al quantitativo di ioni presenti con quella particolare massa (Nota 13). Le righe, per quanto grande sia la risoluzione dello strumento, hanno uno spessore che determina la capacità di risoluzione dello strumento stesso (Nota 14). La riga del pochissimo ⁴He eventualmente presente sarebbe quindi stata completamente coperta da quella vicinissima e di altezza enormemente superiore relativa al Deuterio. Per ovviare a questo inconveniente gli autori hanno eliminato il Deuterio prodotto dall’elettrolisi facendo passare il gas proveniente dalla cella su degli elementi (NEG = non evaporable getter) in grado di catturare molti gas tra cui Ossigeno e Deuterio e umidità, ma non i gas nobili (tra cui l’Elio) che essendo pochissimo reattivi lo attraversano senza essere catturati (Nota 15a).

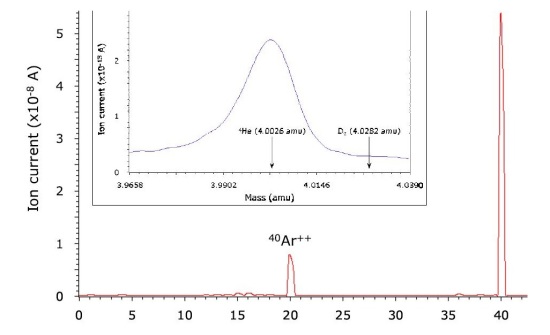
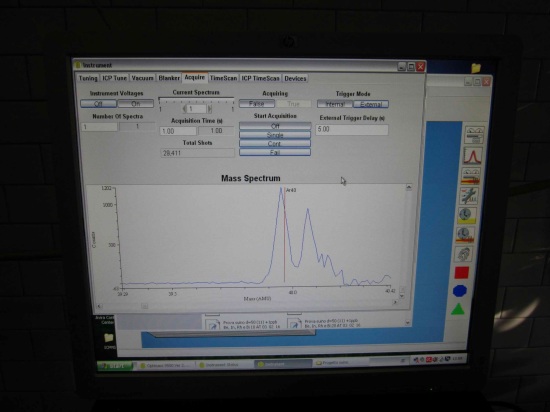
Il procedimento appare corretto, ma qualche dubbio su quanto asserito viene dall’analisi della Figura 4 del Rapporto (che si riferisce a una calibrazione con aria forse addizionata di Deuterio e non a una misura durante un esperimento reale), che riportiamo sotto ingrandita:

Figura 4 del Rapporto 41

In essa si vede, nel riquadro ingrandito, come il picco relativo al Deuterio (4.0282 amu) sia completamente assente, mentre quello relativo all’ ⁴He sia ben visibile. Guardando ai valori in ordinata si vede che il valore corrispondente all’ ⁴He vale 2.5 x 10^-13 A, un valore piccolissimo se confrontato con la corrente relativa all’Argon in prima ionizzazione (amu = 40, I = 5 x 10^-8A): 200.000 volte inferiore. Ciononostante, nel diagramma non ingrandito, tale picco, che dovrebbe essere talmente piccolo da risultare invisibile, si vede chiaramente. Sullo spettrogramma i picchi ad amu 36 e 38 sono generati dagli isotopi dell’Argon, quelli a amu 16, 17 e 18 dagli isotopi dell’Ossigeno, quelli a amu 14 e 15 dagli isotopi dell’Azoto, quelli ad amu 12 e 13 probabilmente dagli isotopi del Carbonio. Evidentemente il NEG non aveva eliminato completamente questi gas (cosa comprensibile, soprattutto per l’Azoto), ma la cosa inspiegabile è che è presente anche il picco a amu 1, attribuibile solo all’Idrogeno, che non poteva essere presente se era effettivamente stato eliminato completamente il Deuterio come mostrato nell’ingrandimento.

La spiegazione più semplice è che il NEG non fosse stato in grado di eliminare completamente né l’Idrogeno (presente forse come impurezza nel Deuterio), né il Deuterio e che il picco mostrato nell’ingrandimento sia traslato a sinistra di 0.02 amu per scalibrazione delle ascisse dello strumento, per cui tale picco fosse relativo al Deuterio e non all’Elio come indicato dagli autori. Questo nel caso che il campione di aria fosse effettivamente stato addizionato di Deuterio (cosa che non compare scritta ma che può essere solo dedotta dalla didascalia ove si dice che il Deuterio era stato completamente eliminato). In un lavoro del 2007 gli stessi autori riportano la stessa immagine (Nota 15b) affermando che l’aria era stata prelevata all’esterno del laboratorio e non era stato addizionato alcun gas. In questo caso è chiaro che il picco si deve riferire effettivamente all’Elio dato che in aria il Deuterio è praticamente assente. Nell’aria però il rapporto tra la quantità di Argon e elio presente è circa 2000, mentre il rapporto indicato in figura è di due ordini di grandezza superiore: occorre supporre che durante quella calibrazione si fosse inspiegabilmente aggiunto all’aria dell’Argon. In ogni caso il fatto che l’unico tracciato riportato dell’analizzatore di massa non si riferisca a un test effettivo, ma a una calibrazione (o meglio a un test con aria senza alcun significato e con un errore nel rapporto Elio/Argon di 100 volte), appare inspiegabile.

Gli autori dichiarano di avere effettuato una accurata calibrazione dell’analizzatore di massa utilizzando miscele con percentuali note di Azoto, Deuterio, Argon e Elio (soprattutto questi ultimi). Dovendo individuare la presenza di Elio ed avere la certezza di non misurare Deuterio, non si capisce perché gli autori abbiano deciso di fare riferimento all’Argon che ha peso atomico 10 volte superiore: fare riferimento al Deuterio ci pare sarebbe stata la scelta più logica e affidabile.

Per avere la certezza che il picco misurato fosse relativo all’Elio e non al Deuterio gli autori avrebbero potuto iniettare, prima di ogni misura, una piccola quantità di Deuterio (paragonabile alla quantità attesa di Elio) all’ingresso dell’analizzatore di massa. In questo modo si sarebbero dovuti vedere i due picchi (uno a 4.0026 amu e uno a 4.0282 amu) e non ci sarebbe stato alcun dubbio a riguardo. Tra l’altro, essendo semplice il dosaggio di precisione di questa quantità di Deuterio, il raffronto tra l’altezza dei due picchi avrebbe permesso una misura quantitativa dell’Elio più precisa, rendendo superflua la delicata e lunga procedura di calibrazione dell’analizzatore di massa con miscele di gas.

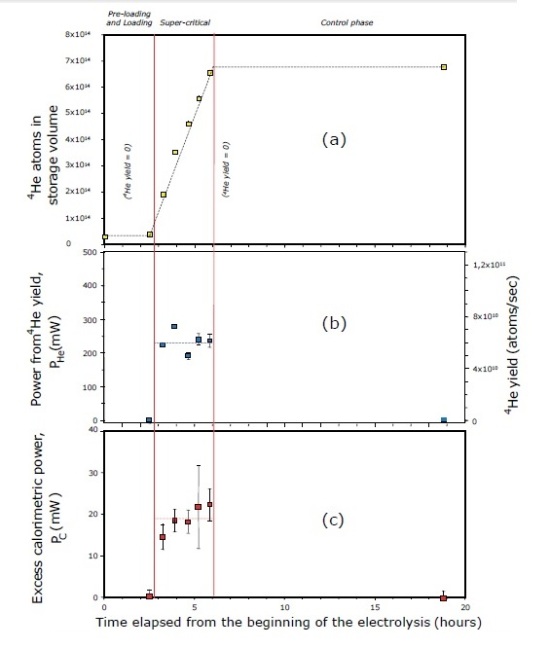
A sostegno del fatto che il picco misurato (ma mai mostrato) attorno ad amu 4 durante la fase supercritica doveva essere proprio quello dell’Elio, gli autori riportano la Figura 9a (Nota 16), nella quale si vede che la quantità di questo gas all’interno del serbatoio di stoccaggio aumentava durante la fase supercritica (durante la quale supponevano essere presenti i fenomeni nucleari), ma era assente durante la fase precedente di precaricamento (durante la quale, essendo il rapporto X < 1, gli stessi autori sostengono che le reazioni nucleari non potevano essere presenti) e rimaneva costante durante la fase successiva di controllo.

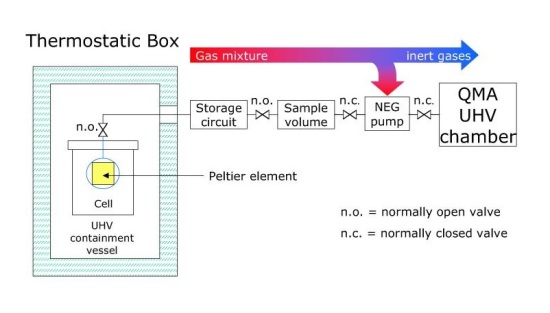
Le nostre possibili spiegazioni sono 2. Durante la fase super-critica la corrente di elettrolisi era circa 5 volte superiore a quella della fase di precaricamento, per cui anche la produzione di Ossigeno e Deuterio erano ugualmente maggiori. Durante la fase super-critica la frequenza delle misurazioni era elevata (una ogni 40 minuti contro una ogni 2 ore e mezza). Il NEG era effettivamente in grado di assorbire tutto il Deuterio generato nella fase di precaricamento e di diffonderlo al suo interno durante la lunga pausa prima della misura successiva, ma durante la fase supercritica per i motivi ora esposti il NEG non era in grado di eliminare completamente il Deuterio di cui restavano tracce, interpretate poi erroneamente come Elio. Il fatto che nella fase di controllo, a elettrolisi spenta, questo gas (non importa se Elio o Deuterio) rimanesse costante all’interno dello stoccaggio, dimostra solo che il contenitore non rilasciava /assorbiva in quantità apprezzabile molecole di tale gas, dal momento che, come si vede nella Figura 1 del rapporto, di seguito riportata, il NEG era posizionato dopo il serbatoio di stoccaggio.

Figura 1 del Rapporto 41

A sostegno del fatto che sia lecito criticare la scelta di utilizzare un analizzatore di massa a quadrupolo in assenza di un picco di controllo di Deuterio, riportiamo quanto scritto su “Vacuum” nel 1998 già citato in Nota 14, in esso si legge:

“The atomic mass of helium differs from deuterium by 0.026 amu only. In order to distinguish a helium leak signal from the large deuterium background due to vessel outgassing. a leak detector with a resolution that is very much beyond the capability of standard mass spectrometry devices would be required. Therefore, special instruments had to be developed. Initially mass spectrometers with the highest achievable resolution in the D2/He mass range, like magnetic sector spectrometers or omegatrons, were used…..Recently, a modified quadrupole was developed at JAERI [Japan Atomic Energy Research Institute, ndr], wich is able to detect a 10^-4 helium peack in a deuterium atmosfere.”

L’analizzatore testato all’epoca allo JAERI era un Balzers Gam 400, tuttora in produzione (seppure in versione aggiornata) e attrezzabile per misure specifiche su Elio e Deuterio.

Se gli sperimentatori usarono un nuovo (per allora) modello di analizzatore appena sviluppato in sostituzione di un analizzatore a settore magnetico considerato all’epoca (ma in realtà ancora oggi) lo strumento di riferimento per questo tipo di misura, avrebbero dovuto scriverlo e avrebbero dovuto mostrare le evidenze della capacità di quello strumento di effettuare con certezza la misura. Invece gli autori non riportano nemmeno il modello dello strumento utilizzato (che noi possiamo solo supporre fosse il Gam 400).

È quindi certo che già all’epoca era disponibile almeno un modello di analizzatore a quadrupolo in grado di effettuare quella misura e possiamo pensare che gli autori abbiano effettivamente utilizzato uno strumento di quel tipo, ma ciononostante è certo che quella misura non è una misura semplice per uno strumento a quadrupolo. Infatti in un articolo molto più recente (Sreekumar, Hogan, Taylor, Turner, Knott “A quadrupole Mass Spectrometer for Resolution of Low Mass Isotopes” pubblicato nel 2010 da Elsevier Inc. per conto di American Society for Mass Spectrometry) si legge:

“To provide adeguate mass discrimination to resolve the peaks of hydrogen and helium isotopes presents certain difficulties. Due to their low mass, these isotopes have a relatively high velocity, wich results in them experiencing a low number of rf cycles in their passage though the QMF and results in poor mass resolution with the average QMS. “

che dimostra come ancora oggi, nonostante gli indubbi miglioramenti avuti sugli strumenti a quadrupolo nei 15 anni che ci separano dalle misure del gruppo De Ninno, occorrano filtri particolari per garantire buone prestazioni su molecole a basso amu.

Ad ulteriore sostegno del fatto che gli Autori possano aver interpretato come Elio quello che in realtà era Deuterio c’è la già citata Figura 9a del documento, che riportiamo di seguito.

Figura 9 del Rapporto 41

In questa figura si può vedere come la quantità di Elio che man mano si andava accumulando all’interno dello “storage”, cresceva in modo quasi perfettamente lineare col tempo (gli Autori tracciano una retta di regressione). Se ciò che gli Autori stavano misurando era veramente Elio proveniente da presunte reazioni nucleari, l’andamento appare strano.

Infatti occorre notare che dal momento dell’ingresso in fase super-critica, secondo le misure effettuate dagli Autori, il rapporto [D]/[Pd] è continuato ad aumentare secondo la curva da essi tracciata in Figura 7, fino a raggiungere il valore corrispondente a un rapporto R/R₀pari a 1. Poichè gli Autori sostengono che le reazioni nucleari iniziano nel tratto di catodo che ha raggiunto per primo questo valore minimo, si deduce che durante la fase super-critica i punti del catodo ove iniziavano fenomeni nucleari dovevano aumentare col passare del tempo, man mano che una parte sempre maggiore di catodo raggiungeva il valore critico [D]/[Pd] = 1. In più si potrebbe supporre che le parti di catodo che per prime hanno avviato le reazioni nucleari (quelle più negative secondo gli Autori), col passare del tempo, raggiungendo valori [D]/[Pd] sempre maggiori aumentassero il numero delle reazioni e/o la loro intensità, come anche sostenuto dagli stessi Autori quando commentano le interruzioni del catodo.

Da questa considerazione ci si dovrebbe quindi aspettare come linea di regressione non una retta ma una curva con concavità verso l’alto. Ma occorre fare un’altra considerazione.

Come si legge a pagina 14 del documento, ad intervalli regolari, durante la fase super-critica veniva prelevato un volume pari al 6.29% del volume dello “storage”. Tali intervalli temporali, come si può vedere il Figura 9 del documento e leggere nel testo, erano pari a 40 minuti. Il documento non spiega nel dettaglio come il circuito fosse fatto, ma asserisce che la pressione all’interno della cella e quindi dello “storage” (che come si vede dalla Figura 1 è in collegamento diretto con essa) veniva mantenuta assolutamente costante e praticamente pari a quella atmosferica, senza introduzione di ulteriore Azoto a parte quello introdotto all’inizio del test.

Poichè durante la fase super-critica la corrente di elettrolisi era di circa 40 mA, la quantità di Deuterio liberato (trascurando quello assorbito dal Palladio che è quantità molto piccola) era di circa 16.7 cc/h. La quantità di Ossigeno liberato era pari a circa 8.3 cc/h. Ammettendo che nessun fenomeno di ricombinazione fosse presente, la quantità di gas che entrava nello “storage” era quindi pari a 25 cc/h.

Dal momento che gli Autori dichiarano che non dovettero immettere Azoto nel sistema durante tutto il corso del test e che lo storage non poteva andare in depressione essendo collegato alla cella elettrolitica che, come asseriscono gli Autori operava a pressione ambiente, ciò significa che la quantità di gas che veniva asportato dallo storage e inviato alla misura non poteva essere superiore a 25 cc/h. Il volume prelevato ogni volta era pari al 6.29% del volume dello storage e venivano effettuati 1.5 prelievi ogni ora. Da qui il massimo volume possibile per lo storage era:

Vs = 25 x 100 / (1.5 x 6.29) = 265 cc

Il documento non riporta quale fosse il volume dello “storage”, ma esso doveva essere composto dalla parte della cella non riempita da elettrolita, dalle tubazioni che collegavano la cella alla valvola di collegamento col volume tarato per il prelievo del campione e, forse, da un piccolo serbatoio aggiuntivo.

Come abbiamo visto il volume dello storage non poteva eccedere i circa 250cc, ma d’altra parte il suo volume non poteva nemmeno essere troppo piccolo o la pressione al suo interno nei periodi tra un prelievo e il successivo sarebbe salita eccessivamente e si sarebbe reso necessario evacuare gas mediante una valvola a sfioramento. E’ quindi ragionevole pensare che gli Autori abbiano adottato un volume di sample prossimo al limite massimo consentito, cioè circa 250cc..

L’atmosfera all’interno dello “storage” cambiava quindi durante il progredire del test, passando da puro Azoto, a una miscela di Azoto, Deuterio, Ossigeno e, secondo gli Autori, una piccolissima quantità di Elio.

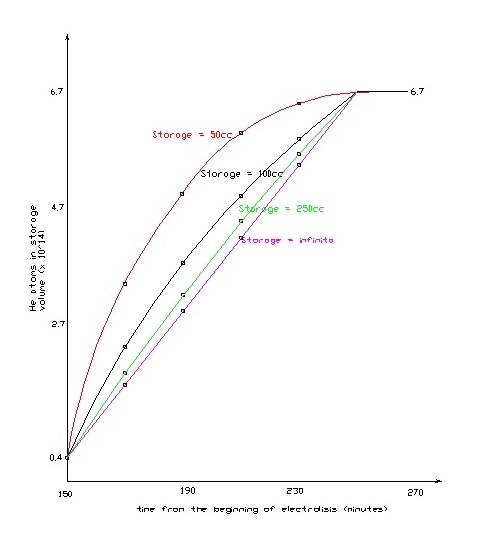
Appare chiaro che per il tempo tendente all’infinito l’atmosfera all’interno dello “storage”, qualunque sia il suo volume, tende a una miscela di composizione costante contenente il 67% di Deuterio, il 33% di Ossigeno e, forse, una quantità piccolissima di Elio. Una produzione costante di Elio non avrebbe dato quindi origine a un aumento lineare della sua concentrazione all’interno dello “storage”, ma a un aumento che asintoticamente si sarebbe avvicinato a un valore costante. In Figura 1bis abbiamo rappresentato l’andamento della quantità di Elio all’interno dello “storage” nel caso di volume di 250, 100 e 50cc.

Figura 1bis

Come si vede con un volume di storage pari a 250cc la curva è già molto vicina a una retta ma presenta ancora una piccola concavità verso il basso che è effettivamente visibile nei dati riportati in Figura 9a.

L’andamento quasi lineare riportato dagli Autori sarebbe quindi compatibile con l’ipotesi che ciò che si stava misurando fosse veramente Elio ammesso che il numero di reazioni fosse costante per tutta la durata della fase supercritica, cosa su cui abbiamo già avanzato i nostri dubbi. In realtà si può fare anche un’ulteriore considerazione.

Il catodo di Palladio, del peso di circa 1 mg, conteneva circa 5 x 10^18 atomi di Palladio. Se il caricamento era circa X = 1, significa che c’erano anche circa 5 x 10^18 atomi di Deuterio. Dalla fig. 9a si deduce che si formavano circa 2 x 10^14 atomi di Elio ogni ora. Dopo un test come quello indicato, della durata di circa 3 ore, erano stati prodotti all’interno del catodo circa 5 x 10^14 atomi di elio, cioè era presente solo 1 atomo di Elio ogni 10 mila atomi di Deuterio. Ci si dovrebbe chiedere per quale motivo gli atomi di Elio uscissero immediatamente per essere misurati dagli Autori, invece di rimanere intrappolati nel reticolo del Palladio per tempi lunghi insieme al Deuterio. Quale forza costringeva solo i nuclei di Elio appena formati a farsi strada tra il reticolo del Palladio già saturo di Deuterio, per portarsi sulla superficie e liberarsi nel bagno elettrolitico?

Gli Autori raccontano che dovettero eliminare la pompa del vuoto ad anello liquido perchè l’Elio rimaneva intrappolato nell’olio. Raccontano pure che l’Elio rimaneva intrappolato nelle pareti della camera di misura nonostante lunghi tempi di degasamento ad alta temperatura. Perchè solo dal Palladio l’Elio usciva immediatamente?

Se pensiamo ad un unico atomo di Elio immerso in un mare di atomi di Deuterio all’interno del Palladio, esso avrà una certa probabilità di uscire in un certo tempo. Se gli atomi sono 100, la probabilità che nello stesso tempo un atomo di Elio esca sarà 100 volte superiore o, detto in altro modo, nello stesso tempo usciranno 100 volte più atomi. Se la produzione di atomi di Elio era costante (circa 2 x 10^14 atomi di Elio all’ora), significa che Elio si sarà cominciato ad accumulare all’interno del Palladio, finchè, aumentando il numero di atomi, la quantità di atomi uscenti per unità di tempo ha eguagliato il numero di atomi che si stavano producendo. Una volta terminata la produzione di atomi (fine dell’elettrolisi e X < 1) l’Elio avrà continuato ad uscire in quantità via via decrescente nel tempo.

Tutto questo suggerisce un andamento della quantità di Elio prodotto non costante, ma crescente nel tempo e prolungata dopo la fine della fase ipercritica. Ma anche ciò porterebbe a un andamento in fig 9a non rettilineo come indicato, ma con concavità verso l’alto. Nell’ipotesi che ci fosse stato veramente produzione di Elio, ci sono quindi due motivi per dire che l’andamento che gli Autori hanno indicato con una retta (o meglio con una curva con leggera concavità verso il basso) dovesse in realtà essere una curva con concavità verso l’alto.
Rimane da chiarire se questo stesso andamento sia ugualmente compatibile con l’ipotesi che in realtà si trattasse di Deuterio.

Come già scritto, la composizione dell’atmosfera all’interno dello storage cambiava durante il corso del test, passando da puro azoto a una miscela di Azoto, Ossigeno, Deuterio e, forse, una piccolissima quantità di Elio. All’aumentare della presunta concentrazione di Elio corrispondeva quindi un aumento della concentrazione di Deuterio, che passava dallo 0% iniziale a circa il 15% alla fine della fase ipercritica (nell’ipotesi di storage di volume 250cc). Dal momento che i NEG non eliminano completamente il Deuterio, ma effettuano nel tempo, come qualunque altra pompa del vuoto, una riduzione della sua concentrazione (teoricamente in condizioni ideali occorre tempo infinito per l’eliminazione totale), il residuo, a parità di tempo di esposizione al NEG è proporzionale alla concentrazione iniziale. L’andamento indicato in Figura 1bis è quindi perfettamente compatibile anche con l’ipotesi che si stesse misurando Deuterio.
In realtà l’andamento di Figura 9a avvalora maggiormente l’ipotesi di misura di Deuterio, dal momento che il presumibile aumento di Elio generato a causa dell’aumento del numero e intensità delle reazioni nucleari di cui si è discusso in precedenza avrebbe dovuto deformare notevolmente la curva al punto da cambiarne la concavità.

Nell’ipotesi che si stesse misurando Deuterio, una seconda possibile spiegazione dell’andamento, che non esclude quella precedente, è la seguente: come si vede in Figura 9 del Documento, si effettuò una misura all’analizzatore di massa a inizio della fase di pre-loading, una alla fine di tale fase cioè 2.5 ore più tardi, poi iniziarono le misure durante la fase super – critica, al ritmo di una ogni 40 minuti. Le prime due misure diedero un valore quasi uguale, pari a circa 3 x 10^13 atomi (di Deuterio) perchè le due misure erano molto distanziate e il NEG aveva avuto il tempo di diffondere al suo interno il Deuterio e gli altri gas assorbiti e questo era il valore di equilibrio. Poi le misure successive effettuate con intervallo di tempo quattro volte inferiore avvenivano senza dare il tempo necessario al NEG per la completa diffusione al suo interno dei gas, per cui l’equilibrio veniva raggiunto via via con un maggior numero di atomi di Deuterio nello “storage”.

Possiamo verificare se queste ipotesi sono verosimili calcolando il livello di vuoto cui sarebbero giunti i NEG. Dalla Figura 9a si vede che nei 250cc dello storage rimanevano 7 x 10^14 atomi (presunti) di Elio. Questi atomi erano dispersi in 250cc di una miscela di Azoto, Deuterio e Ossigeno. Il totale delle molecole presenti in quel volume, secondo Avogadro, era di circa 6 x 10^21 per cui una molecola ogni 10^7 era costituita, secondo la nostra ipotesi, da Deuterio residuo. Poichè la concentrazione di Deuterio, come già visto, rappresentava circa il 15%, occorre supporre che il NEG riducesse la concentrazione del Deuterio di 1.5 x 10^6 volte.
I NEG avrebbero dovuto permettere di identificare Elio in una atmosfera di Deuterio con un rapporto superiore a 10^6, mentre, come riportato all’inizio del presente paragrafo, la letteratura di quel periodo parlava di capacità di un analizzatore di massa a quadrupolo accoppiato a NEG di individuare Elio con un rapporto fino a 10^-4.

Occorre osservare che i NEG sono in grado di raggiungere livelli di vuoto estremamente più spinto (l’uso tipico è in tubi a vuoto e display a emissione di campo ove il vuoto tipico è 10^-9 bar, o negli acceleratori ove il vuoto tipico è 10^-12 bar), ma sono sempre utilizzati come “finitori” e elementi per mantenere nel tempo il vuoto, mai come pompe principali. Il vuoto cioè viene sempre effettuato preliminarmente mediante pompe di altro tipo. Il quantitativo di gas che i NEG sono chiamati ad assorbire è in questo modo ridotto, a parità di condizioni, di un fattore almeno 10^5 – 10^6. Cioè un NEG utilizzato come pompa principale in un sistema con volume di 1cc, dovrà essere dimensionato come normalmente è dimensionato un NEG utilizzato per volumi dell’ordine del metro cubo.

Occorre osservare che gli Autori utilizzarono inizialmente una pompa ad anello liquido come pompa principale cui facevano seguire l’assorbimento mediante NEG. Gli Autori sostengono che in questo modo non si trovava Elio perchè esso rimaneva intrappolato selettivamente nel liquido della pompa, per cui hanno deciso di eliminare la pompa. Noi non siamo riusciti a trovare in letteratura questo fenomeno di assorbimento selettivo dell’Elio, ma in ogni caso gli Autori avrebbero dovuto giustificare questa loro scelta sul piano teorico o meglio riportando qualche esempio in letteratura dell’effettiva esistenza del fenomeno. Ancora meglio sarebbe stato se avessero provato a sostituituire la pompa con una pompa a secco che è comunque in grado di realizzare vuoti di circa 10^-6 bar.

Una obiezione che si potrebbe portare alla nostra ipotesi è che solo pochi degli oltre 100 test condotti dagli Autori hanno evidenziato la presenza del picco indicato come Elio. La nostra spiegazione è che i NEG fossero dimensionati al limite, per cui nella maggioranza dei casi essi erano stati effettivamente in grado di eliminare completamente il Deuterio anche quando questo raggiungeva percentuali elevate all’interno dello storage, ma in alcuni casi, per motivi casuali, l’assorbimento dei NEG fosse ridotto e una piccolissima percentuale di Deuterio veniva trasferito nella camera di misura dell’analizzatore di massa per poi essere interpretato come Elio.

In definitiva ci pare che la misura della presenza di Elio non sia stata documentata in modo sufficiente, mentre il dubbio che si trattasse di Deuterio ci pare non possa essere escluso.

D – La misura del calore in eccesso

Il calore in eccesso è stato misurato mediante una cella Peltier commerciale (Nota 17).

Ancora una volta il documento non aiuta a capire come tale misura sia stata effettuata e occorre riferirsi al filmato di Maurizio Torrealta relativo a una intervista rilasciata dalla De Ninno per cercare di capire come stessero le cose.

Figura 2

Figura 3

Figura 4

Foto 2a del Rapporto 41

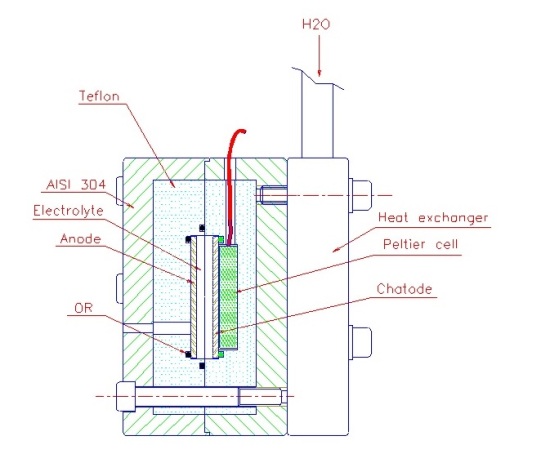
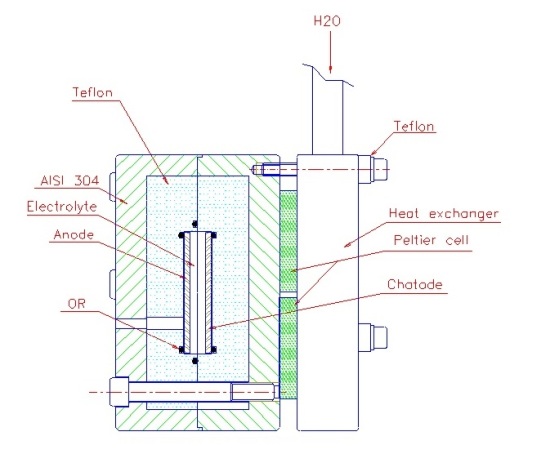
Sulla base delle Figure 2, 3 e 4 tratte da quel filmato e alla Figura 2a del documento che per comodità riportiamo, si può supporre quanto segue:

Il catodo, depositato sotto forma di una sottile pista su un substrato piano quasi certamente ceramico, probabilmente di allumina e di forma quadrata di lato circa 40 mm, era alloggiato all’interno di un blocco di teflon a sua volta contenuto in un contenitore cilindrico in acciaio inossidabile. Tra il blocco di Teflon e il substrato era posta una cella Peltier presumibilmente di dimensioni poco inferiori a quelle del substrato. Il contenitore in acciaio inossidabile scambiava calore con un disco (presumibilmente in ottone) dello stesso diametro mantenuto a temperatura costante mediante canali attraversati da liquido termostatato.

L’anodo di Palladio, quadrato e di dimensione pari a quella del substrato che sorreggeva il catodo, era posizionato parallelamente a 5 mm dal catodo in un blocco di Teflon simile a quello contenente il catodo, ma senza cella Peltier. Il contenitore cilindrico in acciaio inossidabile, diviso in due parti, e il disco in ottone erano avvitati insieme a formare l’intera cella, come visibile nella figura 2a del documento.

Il contenitore in acciaio inossidabile era posizionato all’interno di un vessel ad alto vuoto, di forma cilindrica e dall’apparente volume interno di 1 – 2 litri. Riteniamo che, correttamente, l’utilizzo di tale vessel avesse lo scopo di (quasi) annullare lo scambio termico tra il contenitore in acciaio inossidabile della cella e l’ambiente esterno, in modo da garantire che la maggior parte possibile del calore in uscita dalla cella elettrolitica venisse asportato dal fluido di raffreddamento circolante nel disco di ottone. Esso inoltre garantiva una elevata ripetibilità, rendendo l’esperimento indipendente dalle condizioni ambientali.

Il vessel con tutte le valvole, le tubazioni e i collegamenti elettrici, era posizionato all’interno di una camera termostatata, si suppone, alla stessa temperatura del fluido di termostatazione del disco in ottone garantendo un ulteriore miglioramento della ripetibilità e stabilità del sistema.

La misura della tensione generata dalla cella Peltier è stata trovata essere linearmente proporzionale alla potenza ceduta dalla cella elettrolitica secondo il rapporto 17.3 +/-0.3 mW/mV. Dal momento che la potenza termica misurata in eccesso è stata di circa 20 mW, si deduce che il segnale letto sulla cella Peltier si discostava di circa 1mV dal valore in assenza di reazioni anomale, valore al limite degli errori derivanti dalla deriva della cella Peltier. Si consideri che in quelle condizioni la potenza elettrica immessa nella cella elettrolitica è certamente superiore a 1.4 W (Nota 18), per cui il presunto calore in eccesso era inferiore al 1.5% di quello fornito, valore ritenuto in campo calorimetrico quasi impossibile da misurare con certezza (COP < 1.02) soprattutto su sistemi così piccoli. Ma la cosa fondamentale è che tale quantità di calore rientra negli errori strumentali se si considera che l’incertezza dichiarata dagli stessi autori sul segnale della cella Peltier era pari al +/-1.7%.

Un altro importante fattore di cui gli autori sembrano essersi completamente dimenticati è il problema della possibile ricombinazione dell’Ossigeno e del Deuterio che si liberavano dalla cella e che non venivano tenuti separati in alcun modo (Nota 19).

In base a queste considerazioni, dal momento che il calore in eccesso misurato era 12 volte minore di quello atteso in base alla misura della quantità di ⁴He misurato dall’analizzatore di massa, gli autori avrebbero dovuto prendere in seria considerazione il fatto che non ci fosse alcun calore in eccesso e che quei 20mW di apparente eccesso fossero frutto di errori strumentali o legati alla ricombinazione di Ossigeno e Deuterio. Questo avrebbe dovuto portarli a riesaminare il metodo di misura della quantità di Elio prodotto.

Invece gli autori cercano di dare una spiegazione al fatto che il calore misurato fu molto inferiore a quello atteso, dando per scontato che il valore corretto fosse quello ricavato dalla misura dell’Elio. La spiegazione trovata è sconcertante e oltre ad andare contro i più elementari concetti di scambio termico, sembra indicare che gli autori non conoscessero il principio di funzionamento della misura calorimetrica che essi stessi avevano allestito.

Gli autori infatti ritengono che la misura del calore in eccesso risultasse molto inferiore al reale a causa del fatto che il calore veniva prodotto sul catodo in punti molto localizzati ove la temperatura raggiungeva valori elevatissimi, in qualche caso prossimi a quella di fusione del palladio (1550°C). Secondo gli autori a quelle temperature il calore generato in un punto molto localizzato del catodo si sarebbe trasmesso quasi solo per irraggiamento e la cella Peltier non lo avrebbe rilevato (Nota 20). L’affermazione è assurda perché, se è vero che un corpo in aria a quella temperatura emette calore praticamente solo per irraggiamento, occorre considerare che il deposito di Palladio era di dimensioni micrometriche e in strettissimo contatto termico con il contiguo Palladio freddo e con il substrato, con i quali scambiava calore soprattutto per conduzione, e il tutto era immerso nell’elettrolita (Nota 21).

Un semplice calcolo dimostra l’assurdità dell’affermazione degli autori.

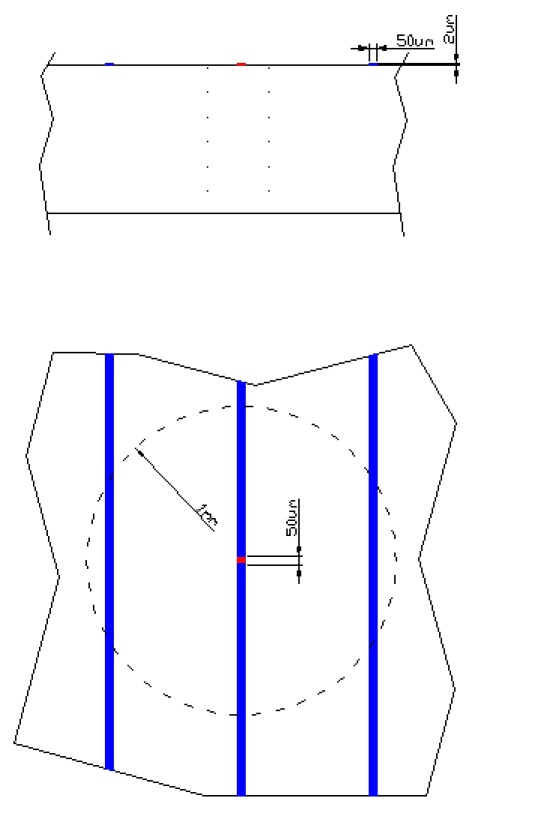
Figura 5

In Figura 5 è schematizzata la sezione della pista in Palladio ed è stata indicata in rosso una ipotetica minuscola zona ove si sarebbe innescata la reazione nucleare esotermica secondo le supposizioni degli autori. Supponiamo che tale area abbia raggiunto una temperatura sufficientemente elevata da cedere fortemente calore per irraggiamento ma non tale da causarne la fusione. Fissiamo questa temperatura in 1200 °C. La conducibilità termica del Palladio è pari a 70 W/mK; la costante di Stefan Boltzman vale 5.7 x 10^-8 Wm^-2K^-4. Supponiamo che la conducibilità termica del substrato sia 25 W/mK (allumina), e che alla distanza di 1 mm la temperatura sia ormai pari a quella dell’elettrolita (22). Trascuriamo cautelativamente il calore scambiato direttamente dalla zona calda con l’elettrolita, e, secondo quanto inspiegabilmente supposto dagli autori, consideriamo nullo il calore scambiato per irraggiamento verso il substrato.

Possiamo scrivere:

superficie irradiante = 2.5 x 10^-9 m²
superficie di scambio per conduzione verso il circostante Palladio = 2 x 10^-10 m²
superficie di scambio per conduzione verso il substrato = 2.5 x 10^-9 m²

da cui:

Q₁ = calore per irraggiamento = 5.7 x 10^-8 x 2.5 x 10^-9 x 1500⁴ = 7.5 x 10^-4 W
Q₂= calore per conduzione verso il Palladio = 70 x 2 x 10^-10 x 1200 / 10^-3 = 1.6 x 10^-2 W
Q₃ = calore per conduz. verso il substrato = 25 x 2.5 x 10^-9 x 1200 / 10^-3 = 7.5 x 10^-2W

Quindi: Q₂ + Q₃ > 100 x Q₁ cioè il calore ceduto per conduzione è 2 ordini di grandezza superiore a quello scambiato per irraggiamento.

Inoltre la cella elettrolitica era un piccolo contenitore chiuso e in qualunque modo il calore venisse generato al suo interno, esso veniva ceduto all’elettrolita che a sua volta lo cedeva a tutte le pareti della cella che a causa dell’elevato coefficiente di scambio termico si trovavano a una temperatura quasi identica a quella dell’elettrolita stesso.

In ogni caso, anche ammesso che il calore in eccesso venisse trasferito solo per irraggiamento come suppongono gli autori, non si capisce perché circa metà di esso non dovesse trasferirsi al catodo (se la pista di Palladio era rovente irraggiava in tutte le direzioni, quindi anche verso il substrato freddo). Circa metà del calore in eccesso doveva quindi essere rilevato dalla cella Peltier. D’altra parte anche il valore di calibrazione (17.3 mW/mV) era stato ottenuto in una situazione nella quale buona parte del calore non attraversava la cella Peltier (Nota 23). Ma anche considerando che durante la calibrazione tutto il calore introdotto attraversasse la cella Peltier, la sottostima del calore prodotto in eccesso sarebbe stato di un fattore 2, non di 12 volte (Nota 24).

Abbiamo voluto verificare le affermazioni degli autori mediante un semplice esperimento, la cui descrizione è riportata nella Appendice A. Anche l’esperimento ha dimostrato in maniera evidente l’infondatezza delle asserzioni degli autori.

E – Misura di raggi gamma

Sebbene l’obiettivo dell’indagine fosse scoprire la presenza di Elio e di calore in eccesso, non si può non ricordare che una reazione nucleare D-D produrrebbe raggi gamma da 23.77 MeV nel caso il prodotto di reazione fosse ⁴He, e neutroni nel caso la reazione producesse ³He. Anche supponendo che la prima reazione fosse fortemente favorita e che i raggi gamma venissero assorbiti in grande parte dal reticolo del Palladio e trasformati in calore, è difficile pensare che i moderni rilevatori non sarebbero stati in grado di evidenziare la presenza di raggi gamma o di neutroni: gli stessi autori, nell’introduzione, riportano il fatto che Fleischmann e Pons riferivano di avere rilevato una leggera radioattività proveniente dalla loro cella, fenomeno riportato dalla quasi totalità dei ricercatori che hanno realizzato esperimenti su sistemi D-Pd, ma anche da chi ha indagato su altri sistemi (Idrogeno – Titanio; Idrogeno – Nichel).

La reazione D-D verso ⁴He in condizioni usuali produce un fotone gamma da 23.77 Mev che è estremamente penetrante: occorre una parete di acciaio dello spessore di molti centimetri per assorbire la metà dei fotoni incidenti, una parete di alcuni metri di Teflon, una parete di decine di metri di polistirolo espanso, che sono i materiali che circondavano la cella in esame.

Consideriamo il numero di fotoni prodotti, secondo gli Autori, all’interno della cella, corrispondenti alla produzione di ⁴He misurato. Dalla Figura 9a si ricava che tale valore era di circa 2 x 10^14 fotoni/ora, corrispondenti a circa 5 x 10^10 fotoni al secondo.
La struttura che costituiva e circondava la cella costringeva tali fotoni ad attraversare uno spessore di circa 10mm di Teflon, 10mm di acciaio inox, alcune decine di centimetri di polistirolo espanso. Come scritto sopra tale schermatura ha effetto schermante quasi nullo su fotoni da 23.77 Mev, ma per sicurezza consideriamo che sia in grado di attenuarli di un fattore 5.
In assenza dei fenomeni supposti da Preparata (Nota 28) tali per cui i fotoni emessi venivano assorbiti dal reticolo del Palladio, i fotoni uscenti dal sistema di prova dovevano quindi essere almeno 10^10 al secondo.
Supponendo di posizionare un sensore di gamma all’esterno del sistema, esso si troverebbe a una distanza dell’ordine di 1 metro dalla cella. La superficie della sfera di spazio a questa distanza è circa 10^5 cm2. Se si utilizza un comune sensore gamma con superficie utile di 1 cm2, esso rileverebbe 10^5 fotoni al secondo. Se anche solo un fotone su 100.000 fosse sfuggito al fenomeno supposto da Preparata di assorbimento da parte del reticolo di Palladio, il rilevatore avrebbe registrato un evento al secondo.

Il numero di fotoni nell’intorno di 23 Mev dovuti al fondo naturale è di uno ogni qualche ora quindi migliaia di volte inferiore. Ci sembra quindi che la ricerca di raggi gamma fosse non solo opportuna, ma doverosa (e certamente nel laboratorio ENEA la strumentazione opportuna non mancava).
Occorre inoltre considerare che un operatore a 2 metri dal dispositivo, in assenza del fenomeno di assorbimento supposto da Preparata, sarebbe stato investito da circa 10^8 fotoni al secondo. La potenza incidente corrispondente è di 3.6 x 10^-4 W. Un operatore presente nel laboratorio avrebbe quindi assorbito una dose di radiazioni corrispondenti a circa 20 mSv/h, una dose importante che avrebbe dovuto essere continuamente monitorata (200 ore di esposizione a quel livello sono mortali).

F – Misura in bianco

Quando si eseguono test di questo tipo è sempre buona norma eseguire test in bianco, invece nel report non ve n’è traccia (Nota 25). Eppure poteva essere eseguito un test in bianco semplicissimo, scambiando la polarità della cella. Il Deuterio emesso sull’elettrodo di Platino non avrebbe ovviamente potuto essere assorbito da questo metallo, per cui non si sarebbe potuto produrre né Elio nè calore in eccesso. Tutto il resto del sistema non si sarebbe potuto accorgere dello scambio per cui un eventuale aumento della quantità di Elio nel serbatoio di accumulo o la misura di un eccesso di calore avrebbe evidenziato un problema sulle misure. Questo test si sarebbe potuto eseguire alla fine di ogni test effettivo (dopo la fase denominata dagli autori Control Phase).

3 – La fusione del catodo

La Figura 10 del documento riporta la fotografia di un catodo in cui sono chiaramente visibili almeno tre interruzioni della sottile pista di Palladio.

Gli autori dichiarano che tali interruzioni non possono essere attribuite a surriscaldamento ohmico per cui sono da attribuire a riscaldamenti localizzati dovuti a intensa reazione di fusione nucleare locale.

In una resistenza elettrica è praticamente impossibile avere più di una interruzione per surriscaldamento ohmico, dal momento che dopo la prima interruzione la corrente si azzera per cui non è possibile che un altro punto possa surriscaldarsi, se non supponendo la perfetta contemporaneità, evento estremamente improbabile. In questo caso però la situazione è completamente diversa: il filamento di Palladio non è una resistenza alimentata alle estremità, ma un catodo alimentato da un solo lato (Figura 3 del documento). In queste condizioni la corrente che fluisce nel filamento del catodo diminuisce dal punto che è collegato al generatore di corrente via via fino ad annullarsi all’estremità opposta. In queste condizioni il punto più soggetto a rottura per surriscaldamento ohmico è quello più vicino al punto di collegamento al generatore, cioè quello più negativo. Anche perché in questo punto la generazione di gas è maggiore, per cui lo scambio termico del conduttore con l’elettrolita è minore. Gli autori dichiarano che la fusione è effettivamente avvenuta in quella zona, ma ne traggono la conclusione che ciò è dovuto al fatto che in quella zona l’effetto Preparata è più intenso, quindi maggiore il caricamento e il calore generato dalla reazione nucleare.

Considerando che gli autori sono certamente riusciti a caricare il Palladio a valori molto elevati, a nostro parere il processo di interruzione multipla del catodo potrebbe essersi svolto nel seguente modo: a causa della forte densità di corrente (400 A/mm²!), nella zona ove la corrente è più intensa (cioè quella più negativa) si origina una interruzione (probabilmente dovuta a distacco della pista dal substrato (Nota 26) a seguito del forte caricamento) e conseguente crollo dello scambio termico col substrato. Questa situazione porta ad un aumento della temperatura del tratto distaccato che per questo aumenta la propria resistenza e quindi la potenza elettrica in essa dissipata (raddoppia circa a 300 °C) e innesca un fenomeno di runaway che porta rapidamente il tratto a interrompersi (Nota 27). La parte rimanente di catodo tra il generatore e l’interruzione continua ad essere attraversata da corrente per cui continua a caricarsi di Deuterio. Occorre notare che la cella era alimentata da un generatore di corrente costante, e non da un generatore di tensione, come si evince dallo schema elettrico visibile nella Figura 3 del documento. Non possiamo sapere se gli autori hanno programmato un limite di tensione sull’alimentatore, ma certamente a seguito della prima interruzione del catodo la tensione applicata alla cella aumentò a seguito del crollo della resistenza elettrica della cella dovuta all’improvvisa diminuzione della superficie del catodo. Questo fatto ha ulteriormente incrementato la produzione di bollicine di gas sul tratto di catodo rimasto alimentato diminuendo ulteriormente il coefficiente di scambio termico con l’elettrolita. Così, dopo un po’ un’altro tratto di pista si distacca e genera una seconda interruzione e così via. La prima interruzione non è avvenuta esattamente all’inizio della sottilissima pista (lungo 1 metro) che costituisce il catodo a causa soprattutto della tolleranza sullo spessore del deposito di Palladio, ma avviene comunque nei primi 5 cm più sollecitati.

Dal momento che gli autori sostengono che invece la fusione era dovuta a intensa reazione nucleare, dovrebbero spiegare come sia possibile che il Palladio sia rimasto carico di Deuterio a valori tali da permettere il mantenimento del fenomeno di fusione nucleare anche a temperatura prossima a quella di fusione (1550°C), quando è sufficiente osservare il diagramma di stato Palladio – Idrogeno riportato in Figura 6 (col Deuterio è quasi identico) per scoprire che ciò appare impossibile dato che a 500°C la pressione di equilibrio è di circa 10.000 bar, un valore molto superiore alla resistenza meccanica del metallo a quella temperatura, con un valore di caricamento pari solamente a 0.7.

Figura 6

4 – Note tecniche esplicative

(Nota 1) Il 6 giugno 2013 alle ore 8:59 sul blog “22Passi d’amore e dintorni“, Antonella de Ninno commentava:

“In questi anni sono arrivata alla conclusione che solo nella migliore delle ipotesi questa ricerca è stata affossata deliberatamente a seguito di un complotto internazionale, in realtà, molto più prosaicamente e tristemente si é trattato di un addensamento di “decision maker” e relativi lacchè nel terzo quadrante del grafico di C.M. Cipolla.“

(Nota 2) “L’inchiesta” di Maurizio Torrealta con intervista ad Antonella De Ninno: FUSIONE FREDDA,RAPPORTO 41- quello che non vi hanno mai detto

Utili alla comprensione anche i seguenti link: Report Fusione fredda (parte 1) e Report Fusione fredda (parte 2)

(Nota 3) Nel 2011 il chimico Camillo Franchini pubblicò una recensione del Rapporto 41, reperibile al seguente link:

https://www.scribd.com/document/63332943/Rapporto-41

oppure direttamente da qui.

(Nota 4) L’Elio-4 è la forma comune dell’Elio. Esso può essere formato mediante fusione nucleare di due atomi di Deuterio, questa reazione con prodotto finale ⁴He (in accordo con la Fisica nucleare GA) risulta però essere molto improbabile, come anche indicato dagli autori nell’appendice teorica del documento; la probabilità che la fusione di due atomi di Deuterio dia origine ad un atomo di Elio-4 è un milione di volte inferiore rispetto alla probabilità di dare origine a Elio-3 più un neutrone oppure a Trizio più un protone.

La figura seguente mostra i branches di fusione DD a più alta probabilità, la fusione DD avviene in due stadi: nel primo stadio si forma un nucleo intermedio eccitato [⁴He*], nella seconda fase il nucleo eccitato rilassa emettendo prodotti di fusione.

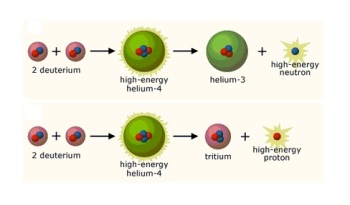Il branch di fusione DD che produce l’Elio-4, il branch meno probabile (10^-6) di seguito raffigurato, ~~ottenuta in acceleratore al di fuori di un reticolo metallico~~ (*), produce oltre al ⁴He un raggio gamma molto energetico (28.3 MeV) e nessun altro prodotto di reazione. Anche in questo caso il processo avviene in due stadi: il primo stadio è comune con il caso precedente e si forma sempre il nucleo intermedio eccitato [⁴He*] ma nella seconda fase il nucleo eccitato rilassa emettendo gamma da 28.3 MeV.

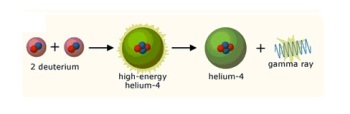I sostenitori della fusione fredda pensano che questo processo di fusione DD con produzione di ⁴He sia il modo di decadimento principale quando la reazione avviene nel reticolo del Palladio. Inoltre suppongono che il raggio gamma non abbandoni il reticolo come sarebbe logico aspettarsi, ma ceda immediatamente la sua energia al reticolo stesso trasformandosi in calore.

(*) GSVIT specifica di non avere trovato ad oggi alcun riscontro, cioè solide prove ed elementi scientifici nucleari-sperimentali (condivisi dalla comunità scientifica mondiale), che costituisca evidenza incontrovertibile delle ipotesi formulate dagli Autori, i quali sostengono esista una fondamentale differenza tra la fusione nucleare del Deuterio nella materia condensata e quella nel vacuo.

(Nota 5) Già in precedenza ci furono tentativi di correlare l’intensità di presunti fenomeni nucleari con il presunto eccesso di calore. In particolare 6 anni prima Yashuiro Iwamura e alcuni colleghi del centro di ricerca della Mitsubishi cercarono una correlazione tra raggi X emessi da un catodo di Palladio e eccesso di calore con un apparato concettualmente simile a quello adottato dall’ENEA. Nella descrizione del loro sistema era indicato anche un rilevatore di ³He, anche se il report finale non riporta alcun dato sulle misurazioni effettuate con tale strumento. Il documento conclude che furono misurati raggi X e eccesso di calore, ma:

“The correlation between excess heat and x-rays has not been made clear under our experimental condition” e “We must investigate further to reach conclusions about the correlation between excess heat and nuclear products”

Non ci risulta che si ottennero mai queste conferme. Una analisi del documento (scaricabile da qui oppure al link: http://lenr-canr.org/acrobat/IwamuraYcorrelatio.pdf) mostra quanto poco consistente fossero le misure di eccesso di calore (dell’ordine del 2% per brevi periodi). L’emissione di raggi X risultò 9 ordini di grandezza inferiore all’attesa.

(Nota 6) Era certamente importante determinare il livello di caricamento del Palladio, ma occorre osservare che non vi è alcun motivo secondo la fisica nota per cui qualcosa debba cambiare quando tale rapporto dovesse raggiungere o superare un determinato valore.

(Nota 7) “Consequences of lattice expansive strain gradients on hydrogen loading in palladium” pubblicato dalla stessa De Ninno su Physical Review B 01-08-1997

(Nota 8) Durante il test di caricamento elettrochimico del Palladio con Idrogeno eseguito da GSVIT si evidenziò come al momento della interruzione dell’elettrolisi, l’Idrogeno cominciasse a gorgogliare violentemente dalla superficie del catodo. In quel caso la pressione all’interno della cavità di misura si ridusse molto lentamente, ma ciò era dovuto al fatto che il Palladio aveva spessore molto elevato (200 volte superiore a quello utilizzato dagli autori) e al fatto che l’Idrogeno contenuto nella cavità (non esistente nel catodo degli autori) costituiva un serbatoio che trasferiva Idrogeno nel Palladio man mano che Idrogeno usciva sul lato bagnato del catodo.

(Nota 9) La tesi, di ben 173 pagine, descrive un esperimento quasi identico, e utilizza una cella quasi uguale ma leggermente più piccola. Le differenze fondamentali rispetto all’esperimento dell’ENEA erano le seguenti:

a – non si fece la ricerca del ⁴He
b – la pista di Palladio, delle medesime dimensioni, era depositata su un substrato di vetro
c – le estremità del catodo erano collegate a un generatore ausiliario di corrente continua
d – non era presente la cella Peltier
e – non era presente fluido di termostatazione
f – la temperatura dell’elettrolita era misurata mediante una termoresistenza (PT100)
g – fu monitorata la temperatura del catodo mediante termocamera

I punti c – f – g meritano una spiegazione:

c – Per garantire l’esistenza di una ddp regolabile ai capi del catodo che permettesse di realizzare l'”effetto Preparata” allo scopo di aumentare al massimo possibile il caricamento, un secondo generatore di tensione era collegato ai capi della pista di Palladio, con il positivo collegato al negativo del generatore che alimentava la cella elettrolitica. Questo secondo generatore era assente nell’esperimento dell’ENEA nel quale la ddp ai capi della pista di Palladio era impressa dalla stessa corrente di elettrolisi applicata da un solo lato del catodo.

f – g – Nell’esperimento di Milano si utilizzò all’inizio solo una PT100 per controllare la temperatura dell’elettrolita e da essa dedurre la potenza erogata per naturale scambio termico del sistema verso l’ambiente. In seguito si aggiunse una termocamera, sfruttando il fatto che il substrato utilizzato per il catodo era di zaffiro trasparente alla radiazione infrarossa nel campo 3-5μm di lettura della termocamera. I due sistemi diedero gli stessi risultati e la termocamera non rilevò nulla di anomalo. Non è chiaro quindi perchè nelle conclusioni del Rapporto 41 si dica che il passo successivo della ricerca avrebbe dovuto prevedere l’adozione di una termocamera.

(Nota 10) Una dettagliata descrizione di caricamenti di fili di Palladio di 50µm di diametro a valori simili a quelli riportati dal gruppo della De Ninno sono riportati su un documento a titolo “Protocollo innovativo per l’iper-caricamento di catodi di Palladio con Idrogeno messo a punto all’ INFN di Frascati. Nuove prospettive per la Fusione Fredda” presentato nel 1998 al LXXXIV Congresso SIF a firma Marini, di Stefano, Celani, Spallone. Nella figura 6b di tale documento è riportata la curva della variazione della resistenza elettrica del filo che indicherebbe un caricamento fino a valori x > 1 e la curva di scaricamento completo. Le affermazioni, trattandosi di un filo e non di un deposito su substrato appaiono più convincenti. Il lunghissimo tempo di scaricamento (16 ore) sembra andare contro la nostra affermazione che il tempo di scaricamento del film utilizzato dal gruppo della De Ninno sarebbe stato di pochi minuti, ma come spiegato nel documento Marini, tale lunghissimo tempo derivava dal particolare elettrolita utilizzato nel suo protocollo, che, a detta dell’autore, avvelenava la superficie del catodo ostacolando la fuoriuscita del gas. Il documento è scaricabile qui oppure a questo link: http://www.lenr-canr.org/acrobat/MariniPprotocollo.pdf.

(Nota 11) Lo schema presenta qualche apparente stranezza (polarità invertita dell’amperometro “I cell”; contatti 7 e 2 del relè apparentemente inutili; resistenza di misura della corrente utilizzata per la misura della resistenza del catodo da soli 10.7 Ω), spiegabili però se si suppone sia stato utilizzato un sistema di raccolta dati con canali tra loro non elettricamente isolati e aventi una impedenza di ingresso non molto elevata.

Dovendo misurare la resistenza del catodo mediante una corrente continua senza che la misura sia alterata dalla conducibilità elettrica della soluzione elettrolitica è opportuno utilizzare la tensione più bassa possibile, in modo da impedire fenomeni elettrolitici (in pratica se si opera al di sotto di 0.2V l’alterazione della misura dovuta all’elettrolita è trascurabile come mostrato nell’appendice C). Una tensione di 0.2V applicata a un catodo con resistenza di 3 kΩ porta a una circolazione di corrente di 67 μA e la corrispondente tensione ai capi della resistenza da 10.7 Ω risulta essere di soli 700 μV. Il sistema adottato assomiglia a quello descritto nella già citata tesi dell’Università di Milano sebbene in quel caso, invece di un generatore di tensione, fu usato un generatore di corrente (150 μA). Nel documento a firma Marini citato in Nota 10 ritennero di risolvere il problema della misura della resistenza del catodo adottando una soluzione elettrolitica più diluita e effettuando la misura mediante un generatore di tensione alternata.

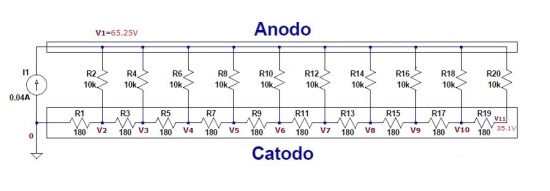
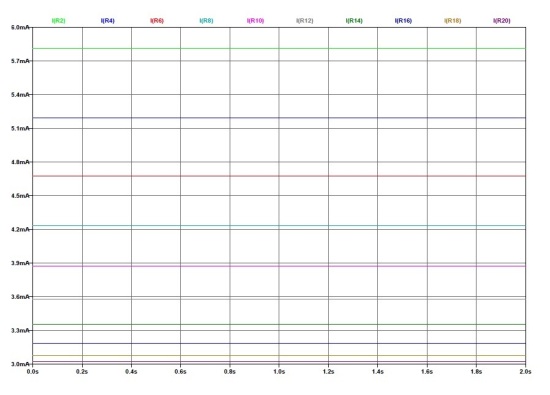
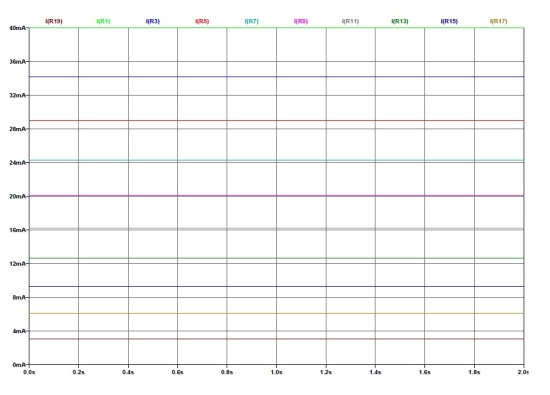
Abbiamo effettuato una semplice simulazione del circuito sulla base dei dati forniti, dividendo la cella in 10 parti. Per mantenere la differenza di tensione ai capi del catodo di 35V e una corrente di elettrolisi di 40mA come indicato dagli autori abbiamo dovuto utilizzare una resistenza di catodo di 1700 Ω, valore ragionevole se si considera una resistenza a catodo scarico di 1000 Ω come deducibile dalle dimensioni geometriche e un fattore di caricamento x = 0.9. Il valore di resistenza del bagno elettrolitico è stato fissato in 1000 Ω in base ai dati di conducibilità del bagno a 20°C e alla forma geometrica della cella, con valutazioni qualitative senza effettuare una simulazione elettrochimica, non possedendo il software necessario. Nella figura sotto sono indicate correnti e tensioni nella cella. Da esse appare chiaro come gli autori siano riusciti ad applicare una consistente differenza di potenziale ai capi del catodo (con lo scopo di innescare l'”effetto Preparata”) utilizzando un solo generatore di corrente. Per contro è chiaro che questo sistema ha portato a caricamento non uniforme del catodo dando origine a probabili errori interpretativi da parte degli autori.

Simulazione

Correnti Elettrolisi

Correnti Catodo

Tensioni

Dalla figure appare chiaro come il valore di tensione ai capi del catodo sia funzione della corrente di elettrolisi, della resistenza del catodo e della conducibilità del bagno. Non è chiaro quindi come gli autori siano riusciti a mantenere tale tensione assolutamente costante (35V) durante tutta la fase supercritica come appare in Figura 8 del documento dal momento che la resistenza del catodo durante questa fase si è dimezzata.

(Nota 12) Gli analizzatori di massa a quadrupolo sono molto diffusi grazie al loro basso costo e alle buone prestazioni. I modelli normali di minor costo non sono in grado di separare ioni con differenza di peso così piccola come lo ione dell’Elio 4 e lo ione del Deuterio, ma esistono modelli, detti ad alta risoluzione, che presentano prestazioni sufficienti. Per questo tipo di misura nei laboratori più attrezzati sono impiegati strumenti di qualità superiore utilizzanti un campo magnetico fisso generato da magneti superconduttori (FT-ICR), che però risultano molto costosi e ingombranti.

(Nota 13) In realtà in ascissa è riportato il rapporto tra peso atomico (in amu, cioè espresso, approssimativamente, come rapporto con il peso del protone) e la carica dell’elemento ionizzato. Per questo, molecole che possono presentare più livelli di ionizzazione danno origine a più righe. L’Argon in particolare dà origine alla riga corrispondente a amu = 40 quando difetta di un solo elettrone (Ar+) e corrispondente a amu = 20 quando difetta di 2 elettroni (Ar++) come visibile in Figura 4 del documento.

(Nota 14) Per separare i picchi relativi all’Elio e al Deuterio occorre uno strumento con potere risolutivo (definito come amu/Δamu) superiore a 200. Tale risoluzione è effettivamente raggiungibile da un semplice strumento a quadrupolo ad alta risoluzione. In Figura 4 del rapporto però i due picchi principali (relativi all’ ⁴⁰Ar) appaiono stranamente larghi per uno strumento ad alta risoluzione. In base alla forma del picco nel riquadro ingrandito, la risoluzione dello strumento si può stimare essere circa 250, quindi sufficiente, seppure al limite. Occorre però ricordare che la risoluzione non ha nulla a che vedere con la esattezza della misura del valore amu che dipende dalla taratura delle ascisse dello strumento. Una taratura non corretta può generare un errore tale da portare a interpretare il picco relativo al Deuterio come picco relativo all’Elio.

Ci siamo recati presso un laboratorio di un istituto di ricerca accreditato (SSICA di Parma) dotato di molti analizzatori di massa di varie tipologie per verificare il normale stato di taratura di tali strumenti. In quel momento era in funzione un analizzatore GBC Optimass 9500 a tempo di volo ortogonale (TOF), la più recente famiglia di analizzatori di massa (inventata alla fine degli anni ’40, ma industrializzato e commercializzato solo a partire dal 2000) visibile in Figura 7.

Figura 7

Abbiamo chiesto alla responsabile di quel laboratorio di mostrarci lo stato di calibrazione delle ascisse (calibrate sull’Argon 40 ogni 6 mesi): l’errore era di 0.03 amu in difetto (Figura 8): se avessimo analizzato un gas contenente Deuterio, quello strumento avrebbe posizionato un picco proprio intorno a amu 4.00 e lo avremmo classificato come Elio 4.

Lo spettro presentato al computer dallo strumento appariva molto meno grossolano di quello mostrato dagli autori in Figura 4 del rapporto: i picchi apparivano come righe molto sottili e solo amplificando notevolmente l’immagine si notava la loro forma triangolare, la cui base aveva una larghezza di circa 0.05 amu. La responsabile ci ha spiegato che a parte la risoluzione dello strumento (che non è uniforme su tutto lo spettro di massa, come ci ha mostrato richiedendo alla macchina di visualizzare la risoluzione calcolata per ogni picco presente, risoluzione che sul picco dell’Argon era 1400), esiste un valore minimo di differenza amu identificabile indipendente dal peso atomico, detto potere risolvente e che per quello strumento era di circa 0.05 amu. Consideravano quindi quello strumento in grado di separare molecole la cui differenza di massa fosse maggiore di 0.1 amu (cioè quello strumento non era considerato in grado di separare sufficientemente i picchi relativi a Deuterio e Elio 4). Nel manuale dell’apparecchiatura si legge che la risoluzione tipica è 2000, ma l’errore sul valore amu è minore di 0.4 amu, cioè 20 volte superiore a quello massimo ammesso per riconoscere l’Elio dal Deuterio.

Figura 8

(Nota 15a) Il procedimento utilizzante i NEG era stato descritto un anno prima dell’inizio dei lavori su “The use of a high-resolution quadrupole gas mass spectrometer system for selective detection of helium and deuterium” “(Christian Day su Vacuum” 1998 /volume 51 / number 1/ page 21 ).

(Nota 15b) Gli stessi Autori del Rapporto 41 insieme a F. Scaramuzzi e C. Alessandrini presentano all’ ICCF8 nel 2000 un lavoro dal titolo: “A New Method Aimed at Detecting Small Amounts of Helium in a Gaseus Mixture” e l’anno successivo all’ ICCF9 gli Autori presentano un lavoro dal titolo: “Experimental Techniques for Dedtecting Small Quantities of ⁴He Gas: Problems and Solutions“. In quest’ultimo si afferma che è stata eliminata la pompa ad assorbimento criogenico e vi si trovano già immagini e parte del testo che verranno poi utilizzati nel Rapporto 41. In questi lavori, come nel Rapporto 41, non si fa cenno all’utilizzo di un doppio sistema NEG.

Sempre gli stessi Autori nel gennaio 2007 pubblicano su “Journal of Vacuum Science & Technology A” un articolo col titolo: “Quantitative detection of tiny amounts of helium isotopes in a hydrogen isotope atmosphere using a standard resolution quadrupole mass spectrometer“. Tale lavoro spiega come sia possibile utilizzare un analizzatore di massa a quadrupolo, persino a bassa risoluzione per misurare piccolissime quantità di Elio in una atmosfera di Deuterio grazie all’utilizzo di due NEG in serie, il primo dei quali del tipo Zr-V-Fe lavorante ad alta temperatura, il secondo del tipo Ti-V lavorante a temperatura ambiente e connesso direttamente con la camera di misura dell’analizzatore di massa. Questa configurazione, a detta degli Autori, consente di eliminare completamente il Deuterio presente, per cui ciò che si misura nei dintorni di amu 4 non può che essere Elio. Seppure non sia scritto in nessuna parte dell’articolo, gli Autori sembrano lasciare intendere che questa fosse anche la configurazione utilizzata durante i test effettuati 5 anni prima e descritti sul Rapporto 41. Questo sarebbe però in contraddizione con quanto indicato sullo stesso Rapporto 41, dove si parla di un singolo NEG, come chiaramente indicato in Figura 1 del documento.

Nello schema riportato in Figura 3 dell’articolo del 2007 si può vedere come sia presente il sistema di valvole che consente di immettere una quantità nota di Deuterio nella camera di misura, che è esattamente quanto abbiamo scritto poche pagine più sopra. Quindi se il sistema utilizzato nel 2001 era quello il cui schema è riportato nell’articolo del 2007, rimane inspiegabile perchè gli Autori non abbiano immesso una piccola quantità di Deuterio nella camera di misura per evidenziare i due picchi di Elio e Deuterio rendendo la misura incontestabile. Si noti come nella pubblicazione del 2007 tale metodologia sia documentata in Figura 8. Se questa configurazione a doppio NEG fu quella effettivamente utilizzata anche nel 2001, considerando che tale configurazione era innovativa, perchè gli Autori non l’hanno scritto chiaramente nè sul Rapporto 41, nè nella pubblicazione successiva?

Un’altra stranezza è rappresentata dalla Figura 10 dell’articolo del 2007: la figura è la stessa riportata col numero 4 sul Rapporto 41, ma la didascalia è diversa: quella del 2007 dice che si tratta di un campione di aria (nel testo si specifica prelevata all’esterno del laboratorio) fatta passare attraverso i due NEG, la didascalia del Rapporto 41 dice che si tratta di un campione di aria dalla quale si deduce come i (solo qui viene usato il plurale) NEG avevano estratto tutto il Deuterio: ma non è chiaro quale Deuterio avrebbero dovuto estrarre se era aria ambiente, che di Deuterio ne contiene una quantità talmente piccola da non poter essere misurata.

(Nota 16) Si noti che la Figura 9 del Rapporto 41 è relativa a un differente esperimento rispetto a quello cui fa riferimento la Figura 8, dato che in un caso la fase supercritica è stata raggiunta in meno di un’ora mentre nell’altro è stata raggiunta in quasi tre ore.

(Nota 17) Usiamo il termine Cella Peltier perché questo usano gli autori, ma riteniamo che potesse trattarsi di una Cella Seebeck, comunemente detta TEG, dal momento che la cella Peltier è progettata per spostare calore mediante energia elettrica, mentre la cella Seebeck, è progettata per generare energia elettrica mediante un flusso di calore, e per quanto molto simili e interscambiabili, nella realtà sono realizzate in modo leggermente diverso allo scopo di massimizzare il rendimento.

(Nota 18) La potenza introdotta sotto forma di potenza elettrica nella cella, trattandosi di corrente continua, è esprimibile come prodotto della tensione applicata (mai indicata dagli autori) per la corrente circolante. Dalla Figura 8 del rapporto e da quanto scritto nel testo si deduce che le condizioni tipiche durante la fase detta “supercritica” prevedevano una tensione certamente superiore a 35 Volt (la nostra simulazione riportata in Nota 11 indicherebbe più di 60V), dato che questa era la differenza di potenziale ai capi del catodo e una corrente di 40 mA, cui corrisponde una potenza elettrica di 1.4 W (circa 2.5W con la nostra simulazione).

(Nota 19) Stranamente il problema era stato ampiamente trattato nella già nominata tesi di laurea in fisica all’università di Milano nell’anno accademico 1999/2000. Gli autori della tesi avevano dedotto che questo fenomeno costituiva la principale fonte di errore nel calcolo della potenza erogata, per cui doveva essere esaminato con grande attenzione.

(Nota 20) Poiché ci è venuto il dubbio che gli autori pensassero che la cella Peltier non fosse in grado di misurare una forma di calore molto localizzata, abbiamo eseguito un semplice test visibile in questo breve filmato.

In esso si vede come due celle Peltier (utilizzate come TEG) poste in serie, anche se di dimensione diversa tra loro, sono in grado di rilevare fonti di calore applicate anche in un piccolo punto di una sola di esse.

(Nota 21) Anche il referee di una rivista cui era stato inviato il rapporto per la pubblicazione mise in dubbio la possibilità che il catodo immerso nell’elettrolita potesse aver raggiunto la temperatura di fusione. Emilio Del Giudice derise tale referee dicendo che evidentemente egli non sapeva che esistono i vulcani sottomarini e che si eseguono saldature anche sott’acqua. In realtà il referee aveva perfettamente ragione (come ha mostrato il nostro semplice calcolo e la nostra semplice dimostrazione descritta nell’Appendice A) ed era Del Giudice che non considerava che non si può paragonare un sistema come quello della cella ENEA con una saldatura ad arco eseguita sott’acqua. In quest’ultima si ha una potenza di alcuni kW concentrata in pochi mm³, mentre nell’esperienza ENEA la potenza è 100.000 volte inferiore. La lava dei vulcani sottomarini può a volte apparire in qualche punto rovente, ma, prescindendo dal fatto che il paragone è inappropriato a causa della enorme differenza di dimensioni, la conducibilità termica della lava è enormemente inferiore a quella del Palladio e nel caso della lava non esiste un substrato che assorbe calore per conduzione mentre lo scambio termico verso l’acqua è in gran parte ostacolato dallo strato di vapore che circonda la lava rovente.

(Nota 22) Se consideriamo un’area di 1 mm di raggio (3 x 10^-6m²) che scambia calore con l’elettrolita, possiamo stimare la sua temperatura media T₁ che avrebbe dissipando 100 mW per sola convenzione verso l’elettrolita a temperatura T₂. Considerando un prudenziale coefficiente di scambio termico convettivo pari a 500 W/m²K e trascurando il calore scambiato per conduzione verso la restante parte di catodo e di substrato, si ha:

T₁ – T₂= 0.1/(1000 x 3 x 10^-6 ) = 66 °C

valore del tutto trascurabile rispetto ai supposti 1200 °C della zona calda.

(Nota 23) In pratica il sistema costituiva un calorimetro isoperibolico con rapporto di cattura del calore molto povero, dell’ordine di 0.3 – 0.4.

I calorimetri isoperibolici misurano la potenza termica emessa da un oggetto posto all’interno di una cavità utilizzando un grande numero di elementi termogeneratori (TEG) disposti su tutta la superficie della cavità, attraverso i quali il calore generato all’interno sfugge verso l’esterno. Gli elementi sono normalmente tutti collegati elettricamente in serie, in modo che ciascuno contribuisce a generare una differenza di potenziale proporzionale al flusso di calore che lo attraversa. La misura è molto poco influenzata dalla posizione ove il calore viene generato all’interno della cavità, a condizione che il calore sia effettivamente costretto a passare quasi unicamente attraverso i TEG. Il rapporto tra il calore che attraversa i TEG e quello totale (cioè quello che attraversa i TEG più quello che riesce a sfuggire senza attraversarli) è detto rapporto di cattura (o efficienza) e in un buon calorimetro vale almeno 0.9-0.95.

Nel caso in esame si può supporre che almeno il 60% del calore non attraversasse il TEG, cioè che il calorimetro allestito dagli autori avesse una efficienza minore del 40%.

I calorimetri isoperibolici sono per quanto possibile da evitare perché, contrariamente ai calorimetri a flusso, non danno una misura assoluta, ma la misura è possibile solo in base a calibrazione che determina il rapporto tra calore e tensione misurata, per cui un errore nella fase di calibrazione può falsare anche in modo notevole tutte le successive misurazioni. Il rischio aumenta grandemente se l’efficienza del calorimetro è bassa. La loro precisione inoltre è scarsa, soprattutto se il rapporto di cattura non è prossimo a 1. La loro semplicità li rende però molto utili in particolari situazioni, soprattutto quando la quantità di calore da misurare è molto piccola o quando occorre un tempo di risposta veloce e non è richiesta una elevata precisione. Grazie al fatto che presentano piccolissima deriva dello 0, sono molto utili nei casi in cui si debba misurare una quantità di calore molto piccola in assenza di calore di “bias”, che invece nel caso in esame è elevatissimo (più di 1 W di bias contro poche decine di mW da misurare).

(Nota 24) Se gli autori ritenevano che il calore in eccesso andasse ad elevare praticamente solo la temperatura dell’anodo posto sulla faccia opposta del contenitore rispetto a quella ove era posta la cella Peltier in modo tale che essa non lo rilevava (il calore da lì avrebbe raggiunto il disco raffreddato di ottone attraverso il contenitore di acciaio inossidabile “by-passando” la cella Peltier), avrebbero potuto porre una seconda cella Peltier dietro l’anodo o più semplicemente avrebbero potuto mantenere l’anodo scostato dal teflon sottostante mediante un sottile strato termicamente isolante (per esempio aerogel) in modo da limitare il flusso di calore verso il contenitore metallico: in questo modo l’anodo avrebbe contribuito al riscaldamento dell’elettrolita e la maggior parte del presunto calore in eccesso sarebbe stato catturato dalla cella Peltier.

(Nota 25) Per prova in bianco intendiamo un test nel quale è utilizzato lo stesso sistema utilizzato per i test reali, ma che, mediante una opportuna alterazione, certamente non sia in grado di erogare potenza in eccesso o ⁴He. Dal momento che gli autori hanno calibrato il “calorimetro” determinando il valore mW/mV generato dalla cella Peltier, certamente devono avere eseguito prove in bianco, ma purtroppo nel rapporto non c’è alcuna descrizione di tale procedimento. Dal momento che durante i test presso l’Università Statale di Milano si realizzò la calibrazione sostituendo il catodo di Palladio con uno in Oro, è ragionevole pensare che anche in questo caso gli autori abbiano seguito lo stesso procedimento. La sostituzione del catodo però rende indispensabile vuotare e aprire la cella, in più, dal momento che il catodo non è più lo stesso, non si può essere certi che i coefficienti di scambio (in particolare con la cella Peltier) siano esattamente gli stessi, per cui, a causa del basso fattore di cattura del calorimetro (vedi Nota 23), la calibrazione sarà soggetta ad un errore di difficile quantificazione.

(Nota 26) La tesi milanese riferisce in vari punti di frequenti e improvvise rotture della pista di Palladio a livelli di caricamento ancora talmente bassi da fare escludere ogni possibilità di innesco di fenomeni nucleari. Questo li spinse a migliorare l’adesione del Palladio al substrato (vetro) mediante un sottilissimo strato di Cromo depositato prima del Palladio. Ciononostante i fenomeni di interruzione non scomparvero completamente. A nostro parere lo strato di Cromo interposto tra il Palladio e il substrato migliorò la situazione non grazie a una migliore adesione del Cromo al substrato, ma principalmente grazie al fatto che il legame metallico instaurato tra Palladio e Cromo costituiva una barriera impenetrabile al Deuterio impedendo che Deuterio ad elevata pressione si frapponesse tra Palladio e substrato causando il distacco. La situazione era cioè analoga a quella realizzata da Paolo Marini (che utilizzò Mercurio) per mantenere carichi catodi filiformi di Palladio come descritto nella sua pubblicazione già citata.

(Nota 27) Anche supponendo che l’elettrolita si interponesse tra il Palladio e il substrato, lo scambio termico si sarebbe comunque ridotto drasticamente dal momento che la conducibilità termica dell’acqua e circa 50 volte inferiore a quella dell’allumina e nello spessore infinitesimo di liquido interposto non avvengono moti convettivi.

(Nota 28) GSVIT non attribuisce particolare attendibilità al cosidetto “effetto Preparata“, lo prende in considerazione in quanto citato ripetutamente dagli Autori del documento e unicamente come conseguente riferimento. GSVIT si occupa del tema partendo dall’analisi dei risultati sperimentali, dei resoconti, sulla base di ciò che viene rivendicato, mostrando dove si manifestano significative incongruenze. Va comunque detto che teorizzare:

a) un canale privilegiato di fusione DD → ⁴He + γ (da 23.8 MeV), cioè il canale notoriamente a più a bassa probabilità (range 10^-6) tra tutte le reazioni di fusione DD ordinarie (come anche gli stessi Autori riportano nell’Appendix A del documento, seppur attribuendo la scarsissima probabilità riferibile alle condizioni di fusione “in vacuo“)

b) che tale canale diventi l’unico possibile nel 100% degli eventi di fusione DD in questi test, cioè che non possa manifestarsi alcuna eccezione che determini anche una produzione di Trizio o di Neutroni

c) e che inoltre tutti i Gamma da 23,8 MeV (raggi altamente penetranti) generati dalle fusioni DD rimangano strettamente confinati nel sottile strato di Pd, per poi essere tutti “energeticamente ridotti” fino a divenire soft X-Rays

appare un insieme di ipotesi molto privilegiate, di per sè poco plausibili, ed inoltre niente affatto condivise dalla quasi totalità della comunità scientifica mondiale.

Si noti che nemmeno la radiazione X è stata cercata/misurata dagli Autori.

5 – Conclusioni

Il Rapporto 41, considerato da molti come un punto forte a dimostrazione dell’esistenza di fenomeni LENR, ci pare mostri parecchi punti deboli. La mancanza di correlazione tra la quantità di calore in eccesso misurato (praticamente assente) e la quantità di Elio misurato e l’assenza di qualsiasi misura di tipo nucleare sposta l’attendibilità della conclusione sulla sola misura dell’Elio generato. Ci pare di avere mostrato validi motivi per dubitare del fatto che ciò che gli Autori stavano misurando fosse realmente Elio ma che in realtà si trattasse di residui di Deuterio e di avere dimostrato che alcune affermazioni contenute nel Rapporto sono prive di fondamento, in particolare quelle che riguardano il perchè non si sia riusciti a misurare l’atteso eccesso di calore e quelle che tentano di spiegare le frequenti rotture multiple dei catodi. A nostro avviso le conclusioni tratte dagli Autori sono basate su risultati decisamente dubbi.

Sebbene in genere GSVIT non esprima valutazioni al di fuori dal campo strettamente scientifico, ci pare in questo caso di poter suggerire una nostra interpretazione del comportamento del prof. Rubbia il quale aveva voluto questo esperimento al punto che, come raccontano gli stessi Autori, partecipò personalmente a riunioni e tracciò di suo pugno alcuni dei diagrammi riportati sul Rapporto ma che successivamente interruppe ogni rapporto con gli Autori prima della pubblicazione del Rapporto stesso, dopo i rifiuti alla pubblicazione da parte delle varie riviste cui il lavoro era stato inviato.
A nostro parere il Prof. Rubbia si rese conto, a seguito delle valutazioni dei referees delle varie riviste, che il Rapporto 41 era “fragile” in svariati punti e probabilmente decise semplicemente di cessare la collaborazione prendendo le distanze dal lavoro (ricordiamo che al momento della pubblicazione gli Autori decisero di omettere il suo nome dall’elenco degli Autori, citandolo solo nei ringraziamenti). Siamo convinti che se il Prof. Rubbia avesse potuto mostrare un Rapporto inoppugnabile lo avrebbe senz’altro sostenuto con convinzione.

Appendice A

Verifica sperimentale della possibilità di arroventare un sottile filo metallico immerso in acqua.

Abbiamo voluto verificare la credibilità dell’affermazione degli autori secondo la quale la sottile pista di Palladio costituente il catodo si sarebbe portato a temperature molto elevate, tali da emettere calore principalmente per irraggiamento, fino alla fine a fondersi (1550°C).

Per fare questo, dopo avere eliminata l’ampolla di una comune lampadina, abbiamo sostituito il suo filamento inadatto perché a forma di strettissima spirale, con una filo in costantana da 80 μm di diametro e della lunghezza di 10 mm come si vede in Figura A1. Il filo aveva dimensione superiore ai 50 μm del deposito di palladio utilizzato dagli autori, ma in compenso non aderiva ad alcun substrato in grado di asportare calore. In ogni caso l’esperimento ha avuto solo lo scopo di visualizzare qual è il reale comportamento di fili sottili in queste condizioni.

Figura A1

In Figura A2 è visibile il filo arroventato in aria (temperatura stimata = 600 °C) con una potenza elettrica pari a 2.5W. Il filamento è poi stato tenuto immerso in acqua mentre si aumentava progressivamente la potenza applicata. Come si vede in Figura A3, si è giunti a una potenza di 59 W senza che il filo riuscisse ad arroventarsi, poi, aumentando ulteriormente la corrente, come visualizzato in Figura A4 il filo si è interrotto senza mai raggiungere in nessun punto il colore rosso.

Figura A2

Figura A3

Figura A4

Il semplice esperimento dimostra che l’elevato scambio termico con l’acqua permette di mantenere la temperatura di un filo sottile riscaldato elettricamente ben al disotto della temperatura di fusione pur dissipando una potenza molto elevata (60W su soli 10mm), enormemente superiore ai 250 mW supposti dagli autori. L’esperimento inoltre dimostra che l’interruzione del filo in questi casi non è dovuto a una vera e propria fusione (non si è mai raggiunto nemmeno il color rosso, mentre la constantana alla temperatura di fusione emette luce bianca), ma a fenomeni probabilmente riconducibili alla elettromigrazione, che si manifestano in maniera evidente quando si opera con densità di corrente di molte centinaia di ampere al mm² (chiunque ha esperienza in campo elettronico conosce i problemi di inrush current in resistori a thin-film metallico). La densità di corrente che ha causato in pochi secondi la rottura del filo nel nostro semplice esperimento era di circa 1000 A/mm² . La densità di corrente che dopo molti minuti (forse alcune ore) ha causato la rottura del film di Palladio descritto dagli autori era inferiore ma non di molto, circa 400 A/mm².

Appendice B

Verifica sperimentale della possibilità di realizzare un efficiente calorimetro isoperibolico.

Sebbene gli autori non menzionino né nel testo né negli schemi il fatto che la faccia fredda della cella Peltier fosse a contatto con una superficie termostatata, riteniamo che così dovesse essere. I motivi per ritenerlo sono fondamentalmente due:

1 – Nella figura 2a del documento si notano due tubi collegati alla piastra che sorregge la cella, che riteniamo essere i tubi di ingresso e uscita del fluido di termostatazione.

2 – Se così non fosse, la temperatura della cella avrebbe risentito fortemente del calore introdotto rendendo praticamente impossibile la misura dell’eventuale piccolo calore in eccesso.

Infatti la cella era stata introdotta in un vessel sotto vuoto spinto (gli autori dichiarano addirittura un UHV che significa una pressione residua inferiore a 10^-5Pa, cioè 10^-10bar) eliminando praticamente qualsiasi possibilità di scambio termico per convezione (μW). Se la cella Peltier non fosse stata affacciata a una superficie termostatata, gli unici scambi termici possibili con l’ambiente esterno sarebbero stati quello per irraggiamento e quello per conduzione attraverso i cavi e le varie tubazioni.

Possiamo stimare la temperatura che avrebbe raggiunto la cella nel caso che tutto il calore introdotto fosse stato scambiato per solo irraggiamento. Consideriamo in base alle fotografie i seguenti dati:

– superficie esterna cella = 300 cm²
– emissività (acciaio inossidabile lucido) = 0.5
– emissività superficie interna vessel = 1 (cautelativo)
– temperatura di termostatazione = 25°C = 298 K
– potenza introdotta = 1.5W

Possiamo scrivere, per la legge di Stefan – Boltzmann:

1.5 = 5.7 x 10^-8x 300 x 10^-4 x 0.5 x [T⁴ – (298)⁴]

da cui si ottiene T = 313.3 K = 40.3°C

Possiamo stimare la temperatura che avrebbe raggiunto la cella nel caso che tutto il calore introdotto fosse stato scambiato per sola conduzione attraverso i tubi di collegamento. Consideriamo in base alle fotografie i seguenti dati:

– diametro tubi = 10mm
– materiale tubi: acciaio inossidabile
– lunghezza media tubi tra la cella e il coperchio del vessel: 100mm
– numero di tubi: 3
– potenza introdotta = 1.5W

Si suppone inoltre lo spessore dei tubi = 1mm (spessore tipico per queste applicazioni), per cui la sezione vale 28 mm².Poichè la conducibilità termica dell’acciaio inox vale 17 W/m°C, possiamo scrivere:

1.5 = 17 x 28 x 10^-6 x 3 x (T – 298) / 0.1

da cui si ottiene T = 403 K = 130°C

Come si vede nelle condizioni descritte quasi tutto il calore sarebbe stato scambiato per irraggiamento e la temperatura della cella in condizioni stazionarie sarebbe stata di circa 40°C. Se questa fosse stata la situazione non avrebbe avuto senso termostatare l’ambiente esterno al vessel con la precisione del centesimo di grado. Tra l’altro occorre notare che il sistema avrebbe raggiunto le condizioni stazionarie in un tempo lunghissimo avendo una costante di tempo dell’ordine di un’ora, mentre gli autori dichiarano un “tempo di risposta” di 5 minuti.

Dobbiamo quindi supporre che il sistema costituisse una sorta di calorimetro isoperibolico ove solo la faccia della cella in prossimità del catodo era posta in contatto con una cella Peltier mantenuta termostatata sull’altra faccia. In queste condizioni correttamente la temperatura dell’intera cella elettrolitica era molto prossima a quella di termostatazione, ma solo una piccola parte del calore introdotto (o generato) poteva fluire attraverso la cella Peltier e essere così misurato. In Figura B1 abbiamo riportato come era approssimativamente la situazione in base alla descrizione e alle fotografie disponibili. In Figura B2 abbiamo disegnato come invece sarebbe dovuto essere realizzato il sistema.

Figura B1

Figura B2

Come si vede la costruzione sarebbe risultata addirittura più semplice. Il rapporto di cattura che nella realizzazione degli autori è stimabile in circa 0.4, sarebbe stato almeno 0.9. Nella situazione di Figura B2 infatti il calore che non attraversa le celle Peltier è solo quello trasmesso per irraggiamento e per conduzione attraverso i tubi e i collegamenti elettrici.

Mentre il calore scambiato per conduzione attraverso tubi e collegamenti, come mostrato in precedenza, è trascurabile, possiamo verificare che nella situazione di Figura B2 anche il calore ceduto per irraggiamento sarebbe stato molto piccolo e conseguentemente il rapporto di cattura del calorimetro sarebbe stato molto buono e avrebbe permesso una misura della potenza immessa (generata) attendibile.

Per fare questo si è allestito un semplice esperimento come mostrato in Figura B3.

Figura B3

Una cella Peltier commerciale (30x30mm, RS 490-1367) è stata posizionata con una faccia su un radiatore in alluminio in stretto contatto termico mediante pasta conduttiva. Il radiatore è stato immerso in acqua (2 litri) ricoperta da uno strato di olio (100cc) per evitare evaporazione. Una resistenza corazzata da 10 ohm è stata posizionata sulla faccia libera della cella. La resistenza è stata poi sommariamente coibentata per ridurre la potenza dissipata in aria. Un tester visualizzava la tensione in uscita dalla cella. Una termocoppia è stata posizionata in stretto contatto termico mediante pasta conduttiva con la corazza in alluminio della resistenza nel punto più vicino alla cella Peltier.

Il sistema è stato lasciato a riposo per 2 ore per permettere l’uniformarsi della temperatura (T0). La tensione erogata dalla cella Peltier minore di 0.1 mV indicava che la stabilizzazione era effettivamente raggiunta.

Figura B4

In queste condizioni si è alimentata la resistenza mediante un alimentatore stabilizzato, con una corrente di 0.33A in modo da avere una dissipazione P1 = 1W (Figura B4). Si è lasciata stabilizzare la temperatura letta (T1) e la tensione erogata dalla cella (V1) (Figura B5).

A questo punto si è inserito tra la resistenza e la cella Peltier un sottile strato di isolante termico (5mm di polistirolo ad alta densità, λ = 0.03 W/mK Figura B6), senza alterare il valore di uscita dell’alimentatore. Si è lasciata stabilizzare la temperatura letta (T2) e la tensione erogata dalla cella (V2) (Figura B7).

Figura B5

Figura B6

Figura B7

Si è verificato che la temperatura dell’acqua non fosse cambiata (<0.1°C), poi per controllo si è ridotta la tensione erogata dall’alimentatore, fino a trovare il valore di potenza P2 che riportava la temperatura della resistenza a un valore molto vicino al valore T1 (Figura B8).

Figura B8

Si è ottenuto:

T0 = 22.3°C
V0 = 0.1 mV
T1 = 26.3°C
V1 = 126.4 mV
T2 = 37.4°C
V2 = 14.9 mV
P2 = 0.256W

Questi dati ci permettono di determinare in due modi il valore di resistenza termica della cella Peltier da noi utilizzata. Detta Ri la resistenza termica dell’isolante interposto tra resistenza elettrica e cella Peltier; Ra la resistenza termica verso l’aria; Rp la resistenza termica della cella Peltier, considerando la composizione serie/parallelo delle resistenze termiche, con semplici calcoli, dalle prime due misure si ottiene:

Ra = 16.4 °C/W
Ri = 185 °C/W
Rp = 5.3 °C/W.

Utilizzando invece la prima e la terza misura si ottiene Rp = 5.4 °C/W con ottimo accordo.

A questo punto possiamo asserire che se gli autori avessero adottato il setup indicato in Figura B2, la superficie delle celle Peltier sarebbe stata almeno 4 volte superiore a quella della cella da noi utilizzata e la relativa resistenza termica sarebbe stata di circa 1.5°C/W.

Quindi la temperatura dell’intera cella (che date le dimensioni e il materiale utilizzato sarebbe stata praticamente isoterma), dovendo dissipare una potenza di circa 1.5 W, sarebbe stata di circa 2 °C superiore alla temperatura di termostatazione. E semplice calcolare che in queste condizioni il calore ceduto per irraggiamento sarebbe stato circa 150 mW (che si poteva ridurre di 5 volte rivestendo la cella con comune foglio di alluminio che ha emissività circa 5 volte inferiore a quella dell’acciaio inox), garantendo un fattore di cattura del calorimetro isoperibolico superiore a 0.9.

La cella Peltier da noi utilizzata erogava 126.4 mV mentre era attraversata da circa 750 mW termici, per cui il suo segnale, alla temperatura del test, era di 5.9 mW/mV. Gli autori dichiarano per il loro sistema 17.3 mW/mV: se si suppone che la loro cella fosse simile come prestazioni a quella da noi utilizzata, si ricava un rapporto di cattura del loro calorimetro pari a 0.34 che conferma le pessime prestazioni che avevamo dedotto in base alla sua errata costruzione.

Appendice C

Verifica sperimentale dell’influenza della tensione utilizzata per la misura della resistenza del catodo.

Abbiamo verificato come l’utilizzo di una tensione molto bassa (tipicamente 0.2 V) permetta una corretta misura della resistenza di un catodo immerso in una soluzione elettrolitica. Si noti che la maggior parte dei multimetri in commercio permette di effettuare la misura di resistenza a questi livelli di tensione (il sistema, detto comunemente “Low – Ohm”, permette la misura di resistenze montate su circuiti stampati e connesse a giunzioni a semiconduttore senza che la misura venga alterata da correnti circolanti nelle giunzioni).

Per effettuare il test abbiamo utilizzato una normale lampadina da 25W cui è stato tolto il bulbo in vetro e a cui è stato accorciato il filamento in modo da poter eliminare i sostegni metallici intermedi e renderlo più rigido.

La misura della resistenza in aria ha evidenziato come la resistenza aumenti all’aumentare della tensione utilizzata per la misura a causa dell’aumento della temperatura del filamento stesso man mano che aumenta la potenza dissipata. Il valore misurato con tensione di 0.3V, pari a 34.5 Ω come visibile in Figura C1, è molto simile a quello misurato da un multimetro, dato che la potenza dissipata in queste condizioni è di soli 2.5 mW e la temperatura del filamento rimane praticamente quella ambiente (20°C). La misura a 3V è pari a 60.8 Ω, come visibile in Figura C2, valore molto più alto a causa dell’innalzamento di temperatura causato dalla notevole potenza dissipata (150 mW).

Figura C1

Figura C2

Si è poi immerso il filamento in una soluzione satura di bicarbonato di sodio a 22.5°C come visibile in Figura C3 (il grosso induttore serviva unicamente come sostegno per il portalampade) e si è effettuata la misura di resistenza a 0.3V, 3V e 5V.

Figura C3

Come si vede in Figura C4 il valore misurato a 0.3V è praticamente uguale a quello misurato in aria, mentre il valore misurato a 3V (Figura C4) è circa il 10% più basso a causa del fatto che a questo livello di tensione i fenomeni elettrolitici sono già importanti. Il fenomeno è ancora più evidente se si alza la tensione a 5V (Figura C5), con una riduzione del valore letto della resistenza del 20%.

Figura C4

Figura C5

	gsvit su Analysis of the report:…
	Ubaldo Mastromatteo su Analysis of the report:…
	gsvit su Analysis of the report:…
	Jed Rothwell su How to overestimate water flux…
	Giancarlo su Edmunt Storms – Progress…