Stesura del Report in data: 10/01/2015
Pubblicazione: 10/01/2015
Traduzione: 12/01/2015
Avendo recentemente letto un commento (postato nel mail-archive vortex-l e scritto da David Roberson) alla nostra recente misura calorimetrica su pompa a trascinamento magnetico Iwaki MD6, commento che tentava di spiegare la grossa differenza esistente tra la potenza ceduta all’acqua durante il nostro test (4.3W) e quella stimata da Jed Rothwell (0.25W), abbiamo ritenuto opportuno rispondere con questo Post anziché limitarci a una semplice risposta nei commenti, nella speranza che fare chiarezza su queste misure possa essere d’aiuto a chi, con onestà intellettuale cerca di affrontare queste problematiche.
Colui che ha scritto il commento individuava una sua spiegazione nella differenza di diametro del tubo di mandata della pompa utilizzato nel nostro test (5mm) rispetto a quello utilizzato da Mizuno (10mm).
In particolare il commentatore scrive:
…Now our favorite skeptic claims that he is using .5 cm pipe instead of the 1 cm pipe used by Mizuno and does not realize that he is making a major error. But, the area of that pipe is reduced by a factor of 4 since it is exactly 1/2 the inner diameter of the original. With a factor of 4 reduction in area comes an increase in the velocity of the water flowing through it by that factor 4 in order to achieve the same mass flow rate. Every thing else being equal you find that the energy imparted upon the water that is sped up from rest to a velocity that is 4 times that from the first case yields the square of that factor. In which case it is 4^2 which is 16 times.
cioè secondo questo commento, essendo il tubo utilizzato da GSVIT un diametro metà di quello utilizzato da Mizuno, la sua sezione era 4 volte inferiore, per cui la velocità dell’acqua in uscita era 4 volte superiore e dal momento che l’energia cinetica dipende dal quadrato della velocità, l’energia cinetica associata all’acqua in uscita (che per attrito si trasforma in calore) è 16 volte superiore, esattamente il rapporto tra le due misurazioni (4.3W contro 0.25W).
Il commentatore inoltre terminava ringraziando la Matematica che a suo avviso aveva risolto il problema e si congratulava con Jed.
…I love it when the math holds up so well.
Congratulations Jed, you got it right.
Purtroppo dobbiamo disilluderlo. Il suo ragionamento è quello tipico di chi ha delle conoscenze scientifiche ma, quasi certamente per mancanza di esperienza nel campo, analizza i problemi in superficie. Speriamo che queste righe ed il test che abbiamo aggiunto possano convincere lui (e chi fa uso del suo approccio) che la realtà può apparire semplice, ma quasi sempre anche il più semplice dei sistemi, se non osservato con la dovuta profondità, può ingannare e portare a conclusioni errate.
Prima di tutto chiariamo che egli si sarebbe dovuto accorgere del proprio errore dal seguente semplice calcolo basato su pochissimi dati forniti dal costruttore della pompa e già in suo possesso perché pubblicati nel nostro precedente post:
- portata massima pompa = 8 litri/min
- prevalenza massima pompa = 1 metro H2O
Ovviamente la prevalenza diminuisce all’aumentare della portata, e la portata massima è misurata a prevalenza nulla, cioè a bocca aperta.
Noi però, applicando le condizioni più conservative, consideriamo pure di avere contemporaneamente la massima portata e la massima prevalenza contemporaneamente.
La potenza ceduta all’acqua in queste condizioni varrebbe:
P = q * ρ * g * h
dove:
- q è la flow capacity = [(8 x 10^-3) /60] m3/s
- ρ è la density of water @20°C = 998 kg/m3
- g è la standard acceleration gravity = 9.81 m/s2
- h è la differential head = 1 m
da cui P = [(8 x 10^-3) /60] x 998 x 9.81 x 1 = 1.3W
da questo calcolo già si deduce che non è questa la via per spiegare una differenza di 4W.
Volendo eseguire il calcolo delle energie cinetiche associate al getto d’acqua in uscita dal tubo di mandata della pompa come effettuato dal nostro commentatore, supponendo come egli fa che la portata rimanga la stessa nel caso del tubo da 5mm e in quello da 10mm possiamo scrivere:
- velocità acqua in tubo da 10mm = (8 x 10^-3/60)/[(5 x 10^-3)^2 x π] = 1.7 m/s
- velocità acqua in tubo da 5mm = (8 x 10^-3/60)/[(2.5 x 10^-3)^2 x π] = 6.8 m/s
- potenza associata al primo getto = ½ x (8 x 10^-3/60) x 1000 x (1.7)^2 = 0.19W
- potenza associata al secondo getto = ½ x (8 x 10^-3/60) x 1000 x (6.8)^2 = 3.07W
Si noti che questa potenza (rif. 4.) risulta comunque nettamente inferiore ai 4.3W misurati, ma è certamente molto superiore al valore reale visto che si è considerato che la pompa centrifuga potesse erogare contemporaneamente la massima portata (8 litri /h) e la massima prevalenza (1 m). La velocità di uscita calcolata nel caso del tubo da 5mm risulta infatti spropositata (ben 6.8 m/s) e corrispondente (con rendimento 1 dell’ugello) ad una prevalenza di 2.3 metri, mentre la pompa in realtà ha una prevalenza massima di 1 metro.
Per verifica, come si vede nella Figura I, abbiamo riposizionato la pompa con il tubo di mandata da 5mm in modo da verificare l’effettiva velocità di uscita dell’acqua.
Figura I – Pompa posizionata con tubo di mandata da 5mm
Dalla Figura II è possibile constatare che il getto ha una lunghezza di 28cm e il dislivello tra l’ugello e il pelo dell’acqua, ove cadeva il getto, è di 10cm.
Figura II – Getto della Pompa 28cm e dislivello 10cm
Dalla Fisica, utilizzando le note e classiche formule relative al moto uniformemente accelerato, possiamo scrivere:
(a) per il moto in verticale: s = ½ x g x (t^2 )
0.1 = ½ x 9.81 x t^2 da cui è immediato ricavare: t = 0.143 secondi
(b) per il moto in orizzontale: s = v x t
0.28 = v x 0.143 da cui è immediato ricavare: v = 1.96 m/s
e la portata associata vale: Q = π x ((2.5 x 10^-3)^2) x 1.96 = 3.85 x 10^-5 m3/s, quindi solo 2.31 l/min
La potenza associata al getto vale quindi: P = ½ x (2.31 x 10^-3/60) x 1000 x (1.96^2) = 0.074W
La potenza risultante è molto piccola ed è inferiore a quella calcolata per il tubo da 10mm perché anche in quel caso si è considerato che la portata fosse di 8 l/min, mentre i 40cm di tubo da 5mm utilizzati in questa misura (uguali a quelli utilizzati nella nostra prova calorimetrica della pompa) hanno posizionato il punto di lavoro della pompa (circa) nel punto presente nel sistema di Mizuno (che adottava un tubo da 10mm, ma lungo 16 metri), così come era nostra intenzione.
La potenza associata al getto reale, presente nel sistema Mizuno, quindi era circa:
P = ½ x (2.3 x 10^-3/60)x 1000 x (0.49)^2 = 0.0046W.
E’ quindi dimostrato che la differenza di potenza misurata nella nostra misura calorimetrica sulla pompa (4.3W) e quella indicata da Rothwell (0.25W) non è causata dal diametro del tubo.
Questi semplici calcoli sarebbero sufficienti per capire la questione, però vogliamo qui cogliere l’occasione per chiarire quanto avevamo già scritto privatamente a Jed Rothwell su questo argomento, e cioè che in realtà il diametro del tubo di mandata non ha di per sé alcuna influenza sulla potenza ceduta dalla pompa all’acqua, essendo in realtà la potenza ceduta meccanicamente all’acqua pari al prodotto della portata per il valore della perdita di carico nel punto di lavoro della pompa. Come spiegato nella descrizione della precedente prova calorimetrica della pompa, il diametro del tubo di mandata è stato calcolato proprio per avere una perdita di carico (circa) pari a quella del circuito del sistema Mizuno. Se avessimo adottato un tubo dello stesso diametro di quello utilizzato da Mizuno, ma più corto, il punto di lavoro della pompa si sarebbe posizionato a una portata superiore e a una prevalenza inferiore, col risultato di aumentare (seppure di poco) la potenza ceduta all’acqua. D’altra parte non era nemmeno possibile utilizzare un tubo da 10mm di diametro e 16 metri di lunghezza, perché lo scambio termico verso l’ambiente sarebbe stato eccessivo e la misura falsata.
In Figura 1 è possibile vedere le curve tipiche di una pompa centrifuga.
Figura 1 – Curve tipiche di una pompa centrifuga
Come si vede la potenza assorbita (e quindi ceduta al fluido) cresce al diminuire della pressione di mandata ed è massima a bocca libera. La scelta quindi di adottare quel diametro è stata dettata dalla volontà di evitare di misurare una potenza superiore a quella reale. A dimostrazione di questa affermazione è stato rieseguito il test calorimetrico sulla pompa, identico al precedente, ma con tutti i tubi da 10mm di diametro.
Verifica utilizzando un tubo da 10mm di diametro
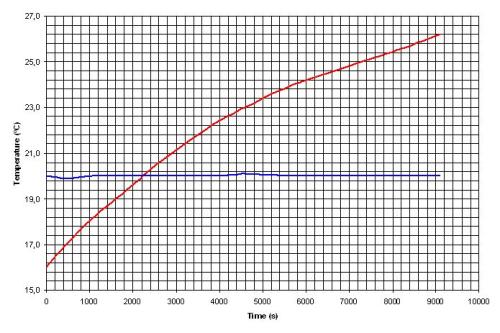
Non trattandosi di un test di particolare importanza (ha solo uno scopo dimostrativo come risposta ad alcuni commenti) non è stata applicata alcuna coibentazione. Questo fatto, unito alla maggiore superficie di scambio dei tubi, spiega perché la relazione delta temperatura/tempo si inclini più del test precedente quando la temperatura dell’acqua supera in modo consistente la temperatura ambiente. In ogni caso anche in questo caso la curva approssima molto bene una retta se non ci si scosta più di un paio di °C da essa, per cui il calcolo è stato eseguito nel campo 18.1°C – 23.0°C, essendo la temperatura ambiente 20.0°C.
In Figura 2 è visibile il nuovo set-up, praticamente identico al precedente.
Figura 2 – Set-up
In Figura 3 è visibile la curva temperatura /tempo durante il test.
Figura 3 – Grafico curva temperatura /tempo durante il test
In Figura 4 è visibile il sistema all’inizio del periodo preso in considerazione nel calcolo della potenza ceduta.
Figura 4 – Temperatura T1 del test
In Figura 5 è visibile il sistema alla fine del periodo preso in considerazione nel calcolo della potenza ceduta.
Figura 5 – Temperatura T2
La potenza P ceduta dalla pompa è:
P = 4183 x 0.800 x (T2–T1) /t
dove:
- 4183 il calore specifico dell’acqua @ 20°C [J/kg°C]
- 0.800 la massa di acqua in riscaldamento [kg]
- T2 la temperatura finale [°C]
- T1 la temperatura iniziale [C°]
- t il tempo tra le due misurazioni [s]
Considerando i valori tratti dalle due fotografie (Figura 4 e Figura 5) effettuate a 1.9°C sotto (la T1) e 2.9°C sopra (la T2) rispetto alla temperatura ambiente e scattate rispettivamente alle ore 08:43:31 e alle ore 09:42:34, cioè a 3543 secondi di distanza, si ha che la potenza ceduta dalla Pompa all’acqua è pari a 4.6W.
Come si vede la potenza è risultata leggermente superiore a quella misurata nel primo test.
In Figura 6 è visibile la misura mediante pirometro della temperatura del motore, che è risultata leggermente superiore a quella del primo test:
Figura 6 – misura mediante pirometro della temperatura del motore
ciò è normale essendo leggermente superiore la potenza erogata, ma è possibile che almeno in parte la differenza sia dovuta a tensione di alimentazione leggermente superiore o a lettura in un punto leggermente più caldo.
Confermiamo quindi la nostra misura della potenza termica ceduta all’acqua dalla pompa.
Poiché Jed Rothwell continua a sostenere che il nostro valore è impossibile, lo invitiamo nuovamente a eseguire lui stesso (o a far eseguire a Mizuno) la misura da noi effettuata, dato che, come abbiamo mostrato, il test non richiede più di 2-3 ore e a pubblicare foto e diagrammi come abbiamo fatto noi.
A questo punto è doveroso chiedersi come sia possibile che la pompa immetta più di 4W nell’acqua, se il lavoro meccanico esercitato dalla pompa sull’acqua, come abbiamo visto, è 20 volte inferiore.
Una prima spiegazione viene dal fatto che queste piccole pompe centrifughe a trascinamento magnetico hanno un rendimento molto basso, raramente superiore a 0.3.
Questo però spiegherebbe una potenza ceduta dell’ordine di 1 – 2W, ma non appare una spiegazione sufficiente per spiegare 4.6W.
La spiegazione (che avevamo già comunicato in privato a Rothwell) è che una quantità non trascurabile di calore fluisce per conduzione dal motore (che come si vede in Figura 6 è a una temperatura dell’ordine di 45°C) all’acqua attraverso la parete dell’accoppiamento magnetico.
Per chiarezza in Figura 7 e 8 è possibile vedere la pompa smontata.
Figura 7 – Pompa smontata e temperatura del trascinatore magnetico
Figura 8 – Pompa smontata
Come si vede chiaramente l’acqua che circonda il magnete si trova a diretto contatto con la sottile parete plastica che all’esterno è in contatto col trascinatore magnetico, la cui temperatura dopo lo smontaggio a fine test era ancora a 42.5°C come mostrato in fig 7.
Queste foto smentiscono quanto Rothwell affermava, cioè che queste pompe sono costruite in modo da impedire ogni flusso di calore dal motore al fluido.
Gruppo Scientifico per la Valutazione Indipendente di Tecnologie 